Tweedegraadsfuncties - De functies f(x) = ax²
De functies f(x) = ax²
In dit deeltje bespreken we de invloed van de parameter a op de grafiek van de functie
f(x) = ax².
We gaan er altijd van uit dat a ≠ 0.
| a > 0 | a < 0 | |
|---|---|---|
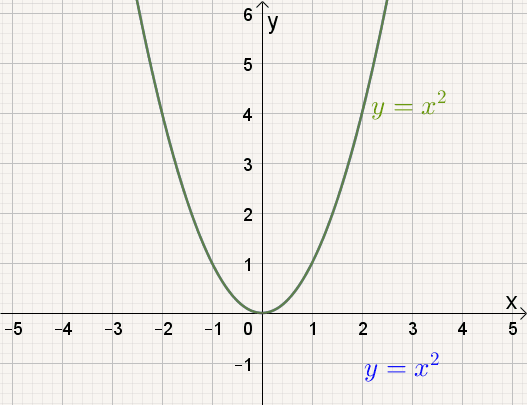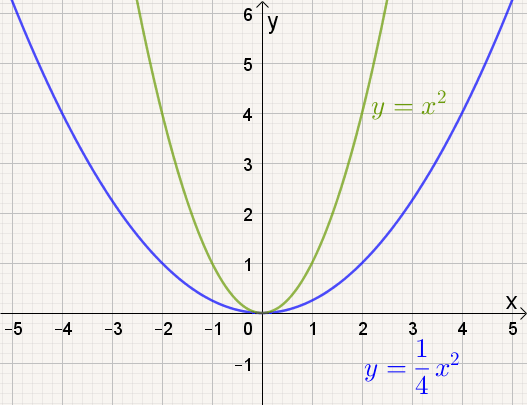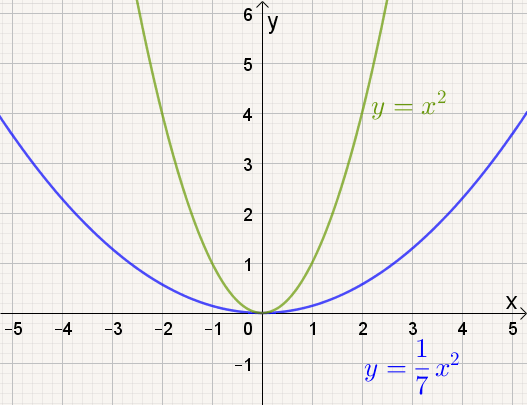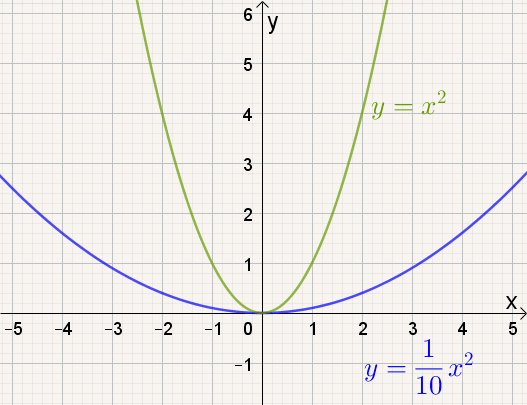
| a toenemend |
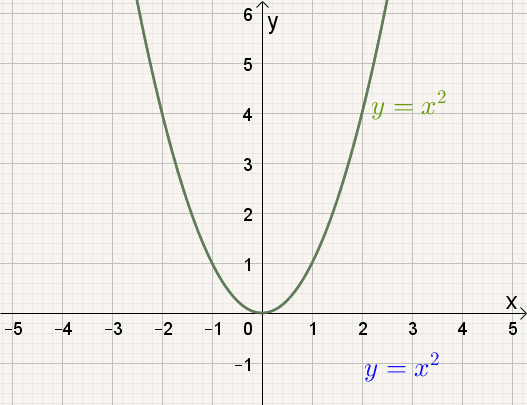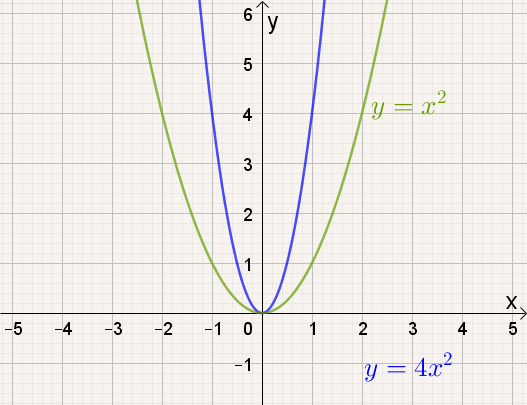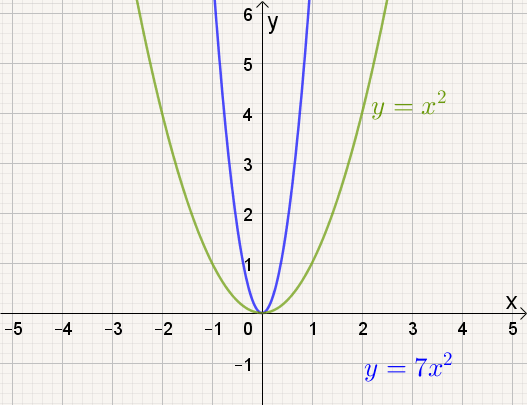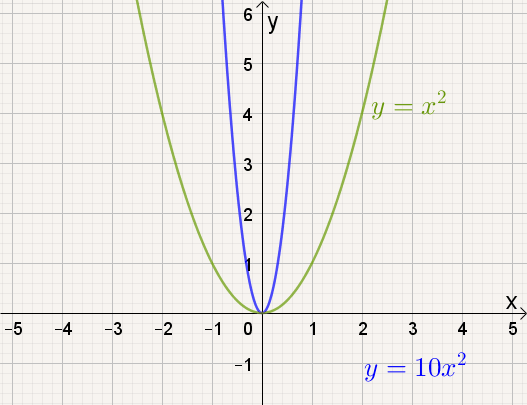
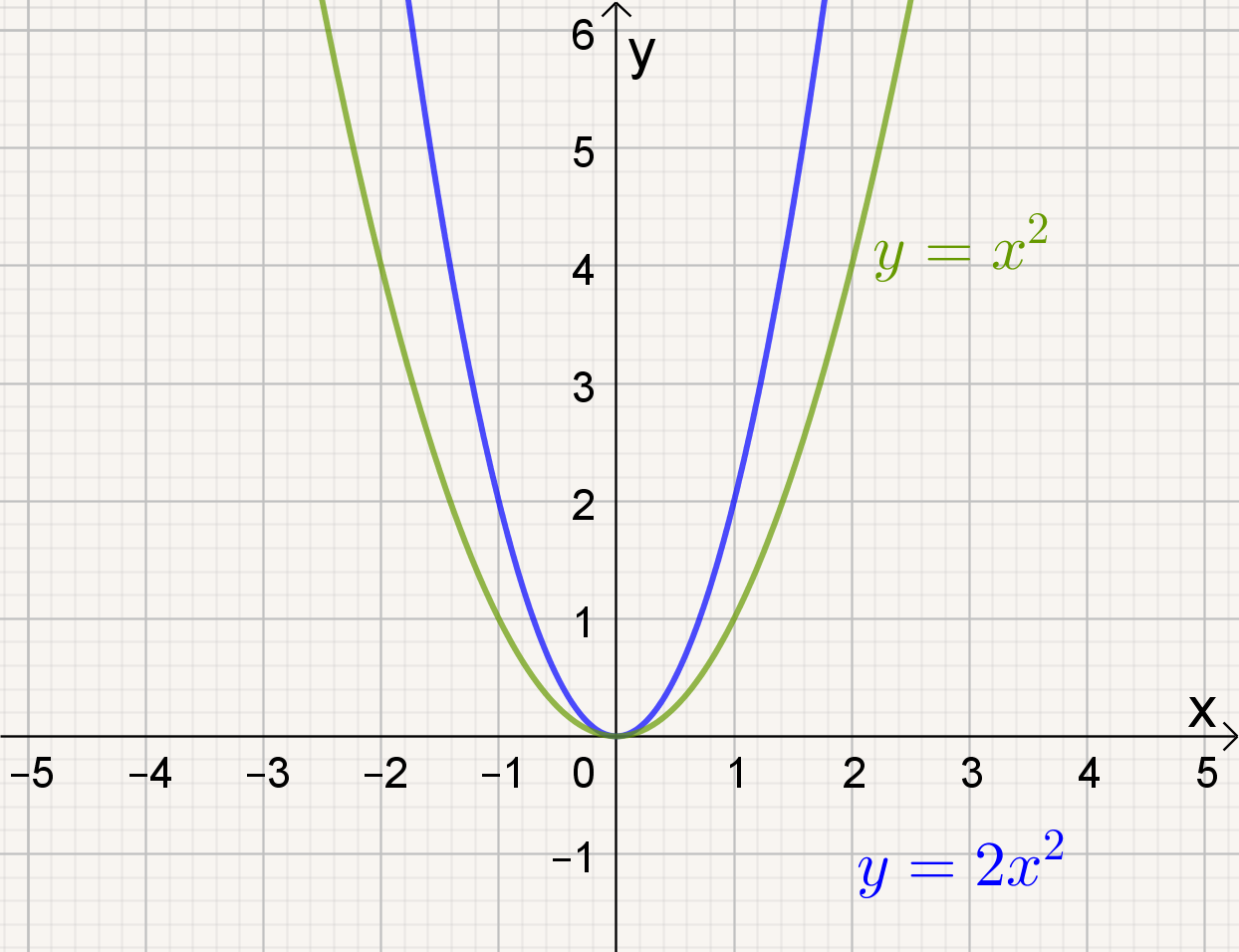
Naarmate a groter wordt, |
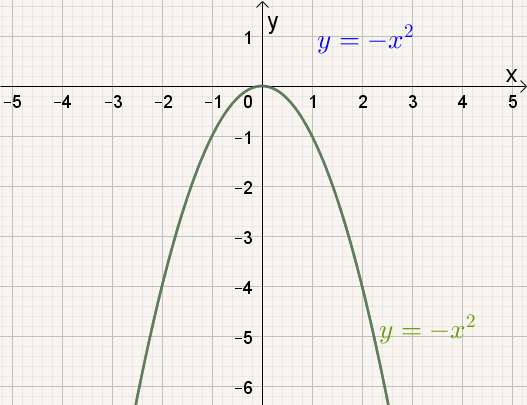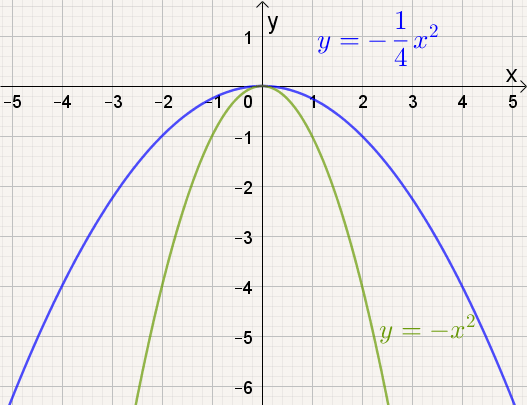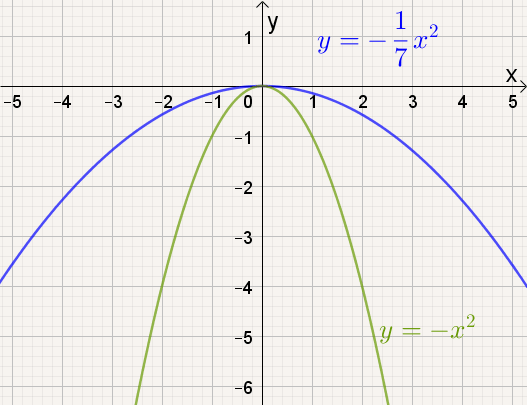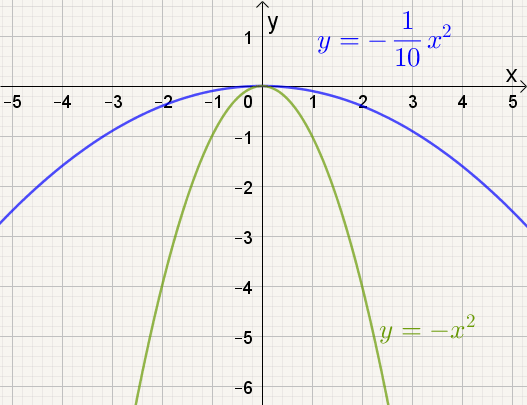
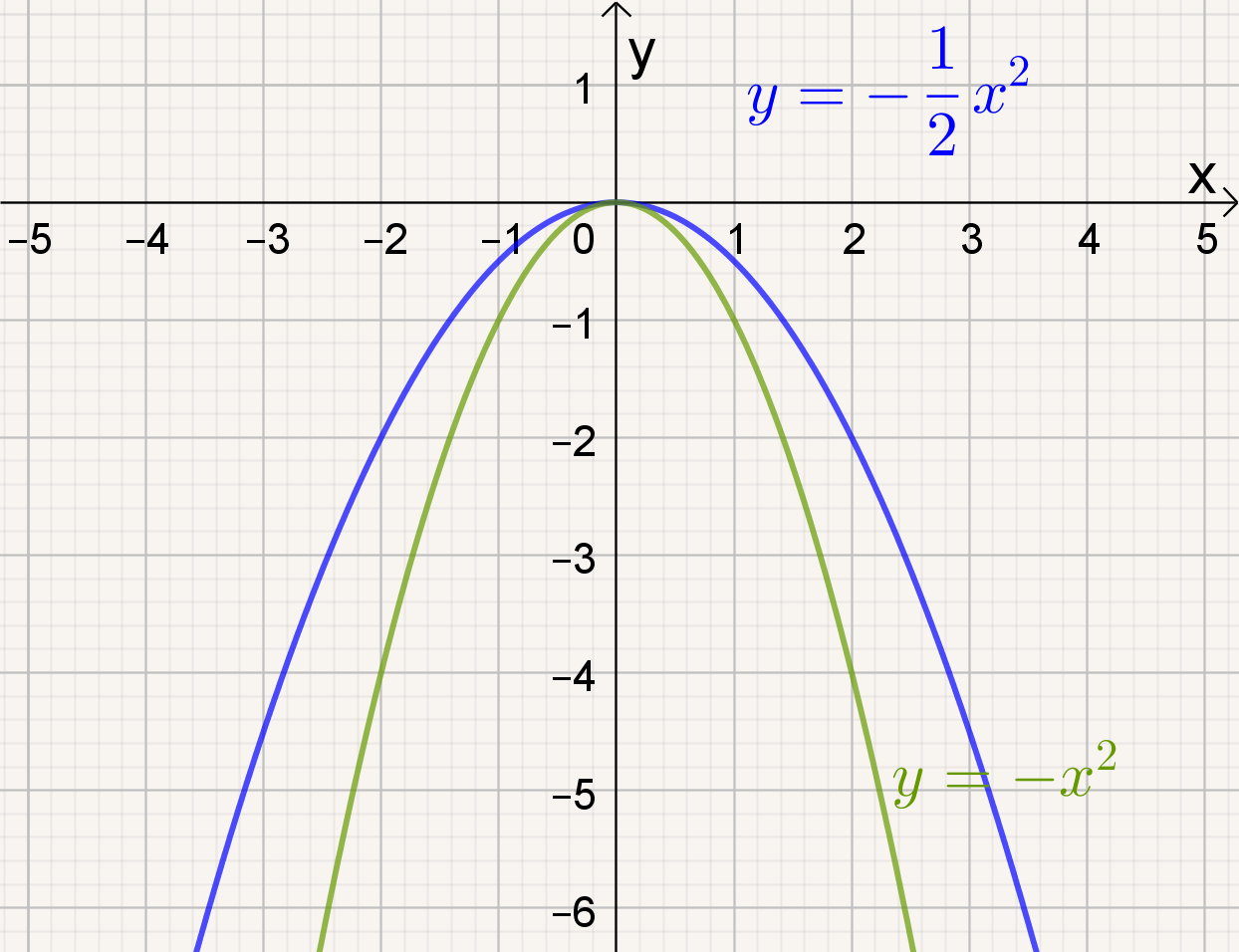
Naarmate a groter wordt, |
| a afnemend |
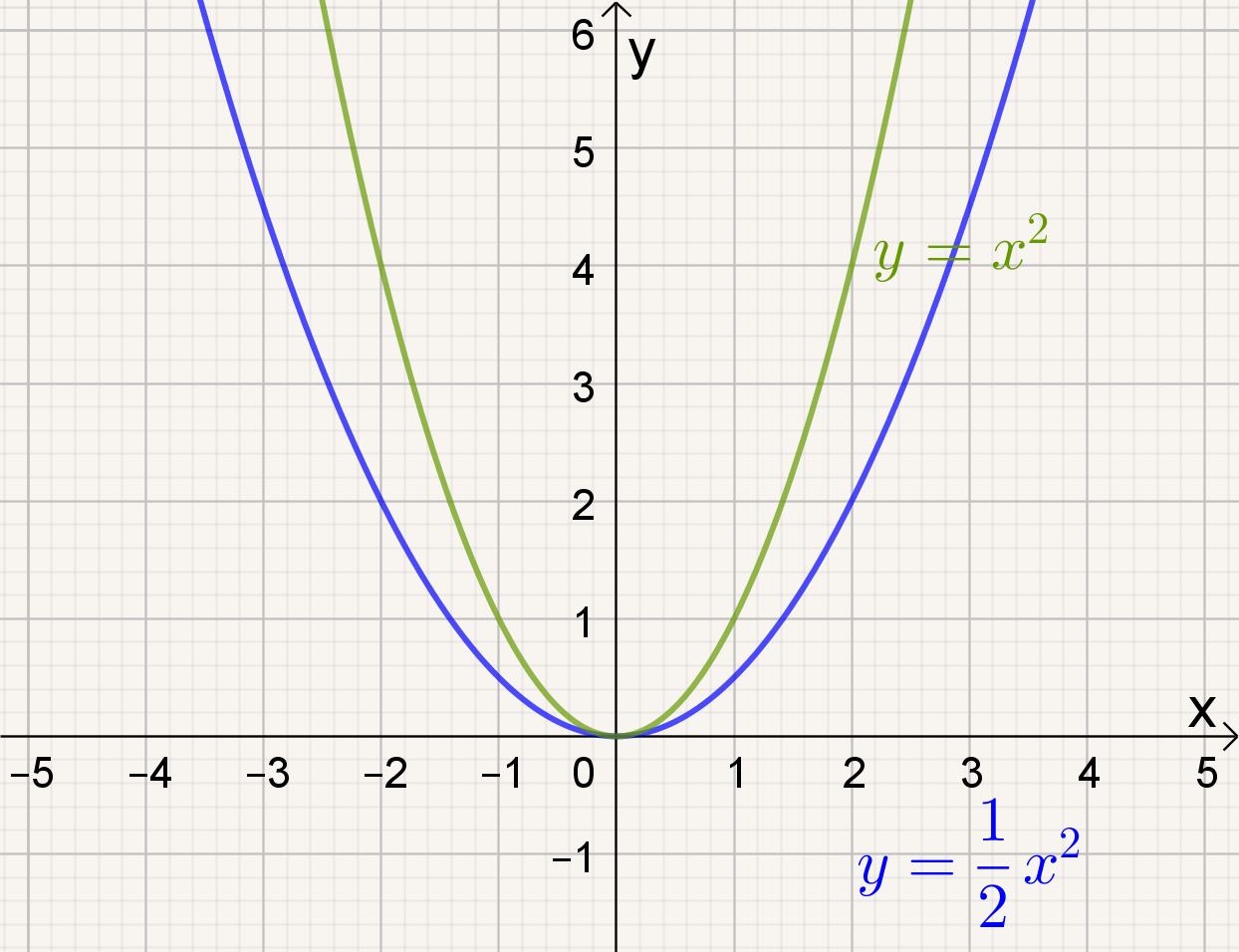
Naarmate a kleiner wordt, |
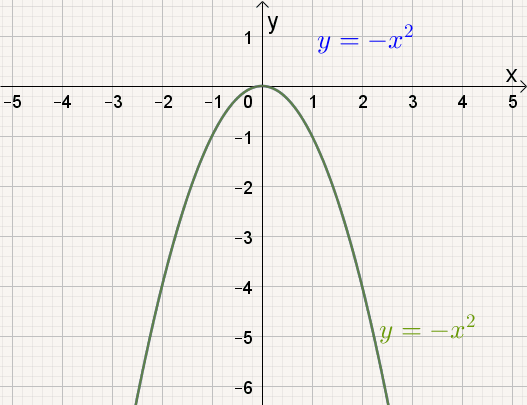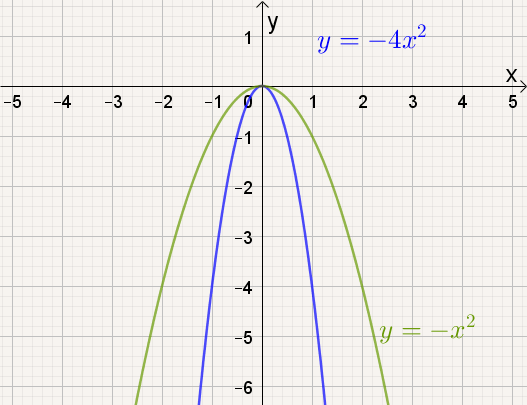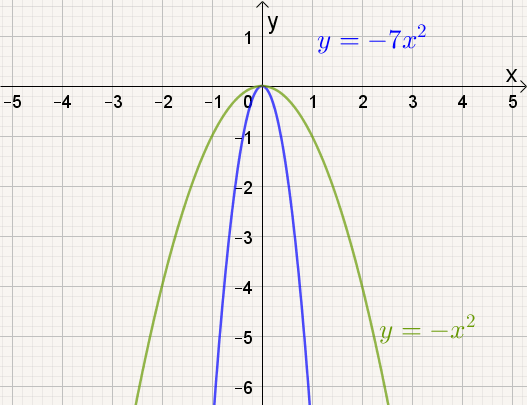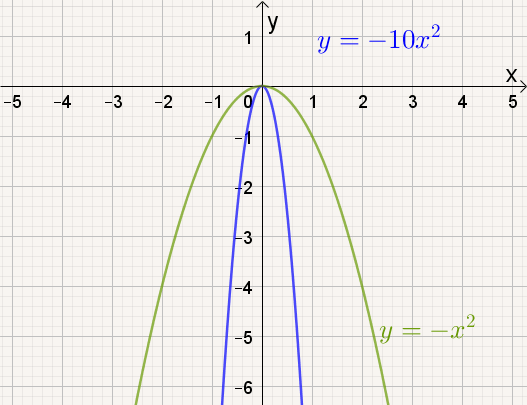
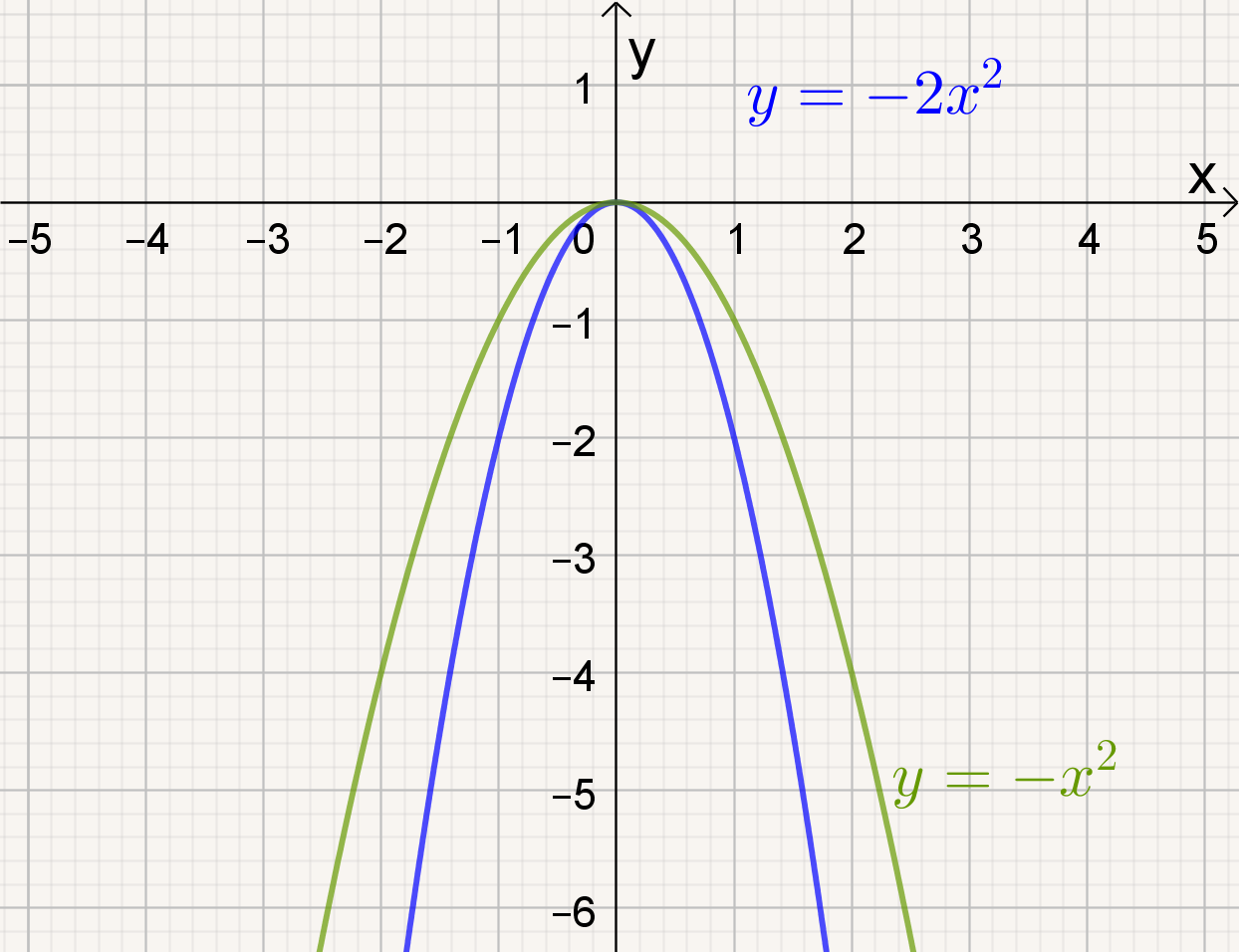
Naarmate a kleiner wordt, |
Dus als a ≠ 0, dan zal
- naarmate |a| groter wordt, de grafiek van f(x) = ax² smaller worden.
- naarmate |a| kleiner wordt, de grafiek van f(x) = ax² breder worden.
We zeggen dat we de grafiek van f(x) = ax² verkrijgen door de grafiek van y = x² verticaal 'uit te rekken' met factor |a|. Is a < 0 moet je ook nog spiegelen om de x-as .
Voorbeelden
We tekenen de grafiek van
 en
en
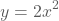 en
en
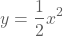 .
.
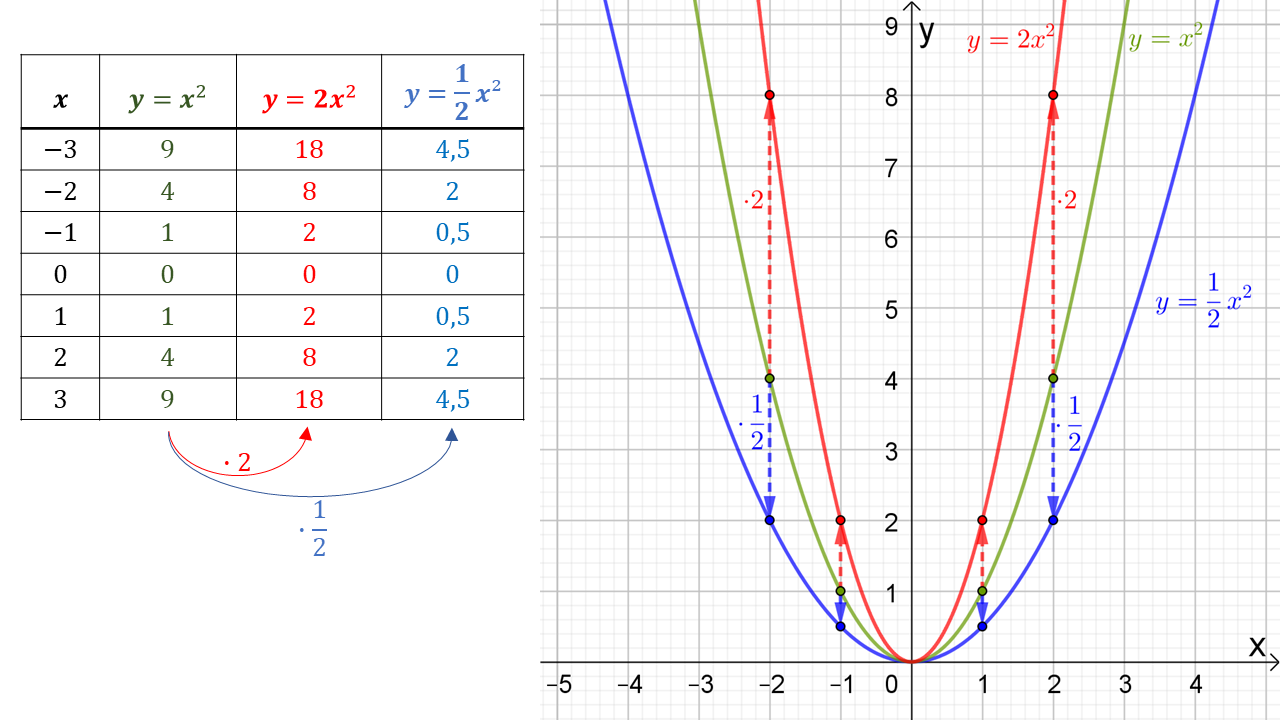
We vergelijken eerst de functiewaarden in de tabel en de grafiek van
 en
en
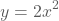 .
.
- Om de grafiek van
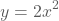 te bekomen, vermenigvuldigen we de y-coördinaat van elk punt van de grafiek van
te bekomen, vermenigvuldigen we de y-coördinaat van elk punt van de grafiek van
 met 2.
met 2.
- We zeggen dat we de grafiek van
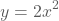 krijgen door de grafiek van
krijgen door de grafiek van  verticaal 'uit te rekken' met factor 2.
verticaal 'uit te rekken' met factor 2.
- De grafiek wordt hierdoor smaller.
We vergelijken vervolgens de functiewaarden in de tabel en de grafiek van
 en
en
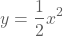 .
.
- Om de grafiek van
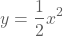 te bekomen, vermenigvuldigen we de y-coördinaat van elk punt van de grafiek van
te bekomen, vermenigvuldigen we de y-coördinaat van elk punt van de grafiek van
 met 1/2.
met 1/2.
- We zeggen dat we de grafiek van
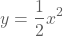 krijgen door de grafiek van
krijgen door de grafiek van  verticaal 'uit te rekken' met factor 1/2.
verticaal 'uit te rekken' met factor 1/2.
- De grafiek wordt hierdoor breder.
We kunnen een gelijkaardig onderzoek doen voor de grafieken van de functies van
 en
en
 en
en
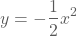 .
.
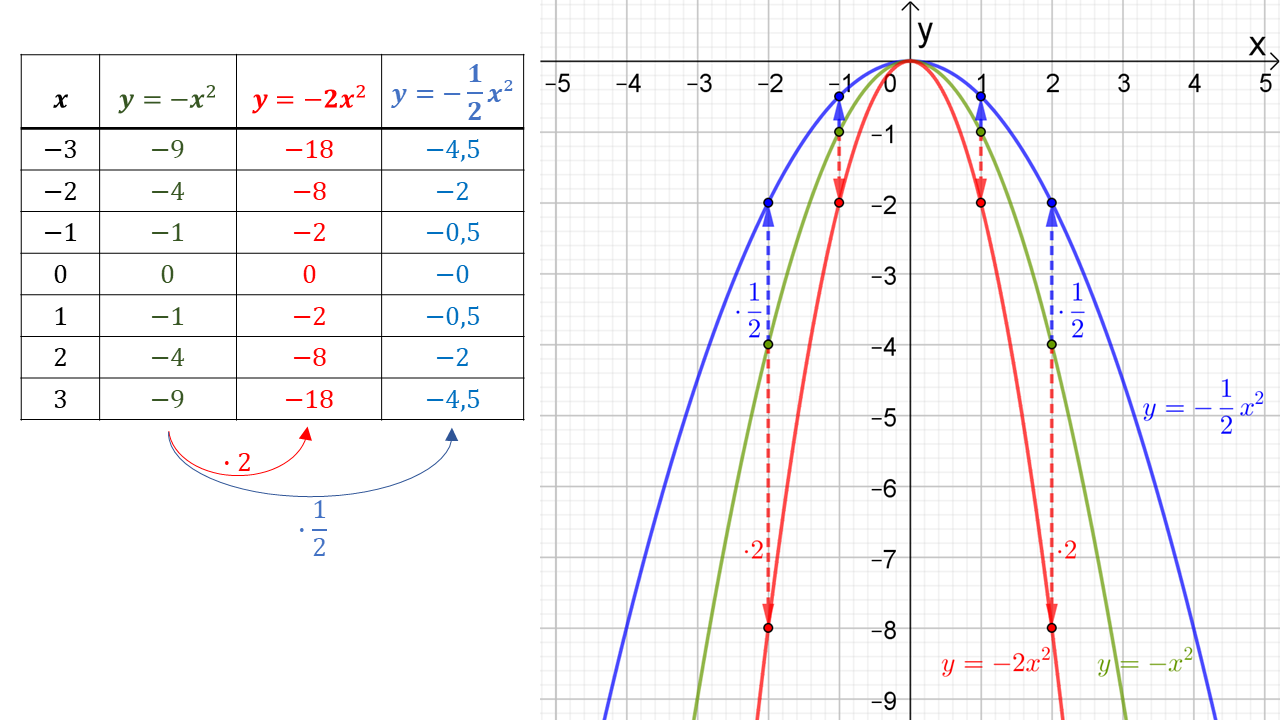
We zullen tot hetzelfde resultaat komen, want deze grafieken ontstaan uit de grafieken van
 en
en
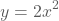 en
en
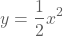 door ze te spiegelen om de x-as.
door ze te spiegelen om de x-as.
Ook de grafiek van de functie f(x) = ax² noemen we een parabolen.
- De top van de parabool is (0,0)
- De symmetrieas van de grafiek is de y-as met vergelijking x = 0.
- Als a > 0, dan is de grafiek van
f(x) = ax²
een dalparabool.
Als a < 0, dan is de grafiek van f(x) = ax² een bergparabool. - Als |a| > 1, dan is de grafiek van
y = ax²
smaller dan de grafiek van y = x².
Als |a| < 1, dan is de grafiek van y = ax² breder dan de grafiek van y = x².
Je kan de grafiek van de functie y = ax² vinden door de grafiek van y = x² verticaal uit te rekken met factor |a| en als a < 0 moet je ook nog spiegelen om de x-as .
