Tweedegraadsfuncties - De functies f(x) = ax² - De functies f(x) = x² en g(x) = -x²

De functies f(x) = x² en g(x) = -x²

De functies f(x) = x² en g(x) = -x² worden tweedegraadsfuncties of kwadratische functies genoemd omdat de hoogste exponent van x in het voorschrift 2 is.

Andere voorbeelden van tweedegraadsfuncties:

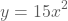
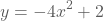
In wat volgt zullen we dergelijke functies bespreken. We bestuderen echter eerst de basisfuncties f(x) = x² en g(x) = -x².

Op basis van de waardentabel tekenen we de grafieken van beide functies.

x	...	-3	-2	-1	1	2	3	...
f(x) = x²	...	9	4	1	1	4	9	...
g(x) = -x²	...	-9	-4	-1	-1	-4	-9	...

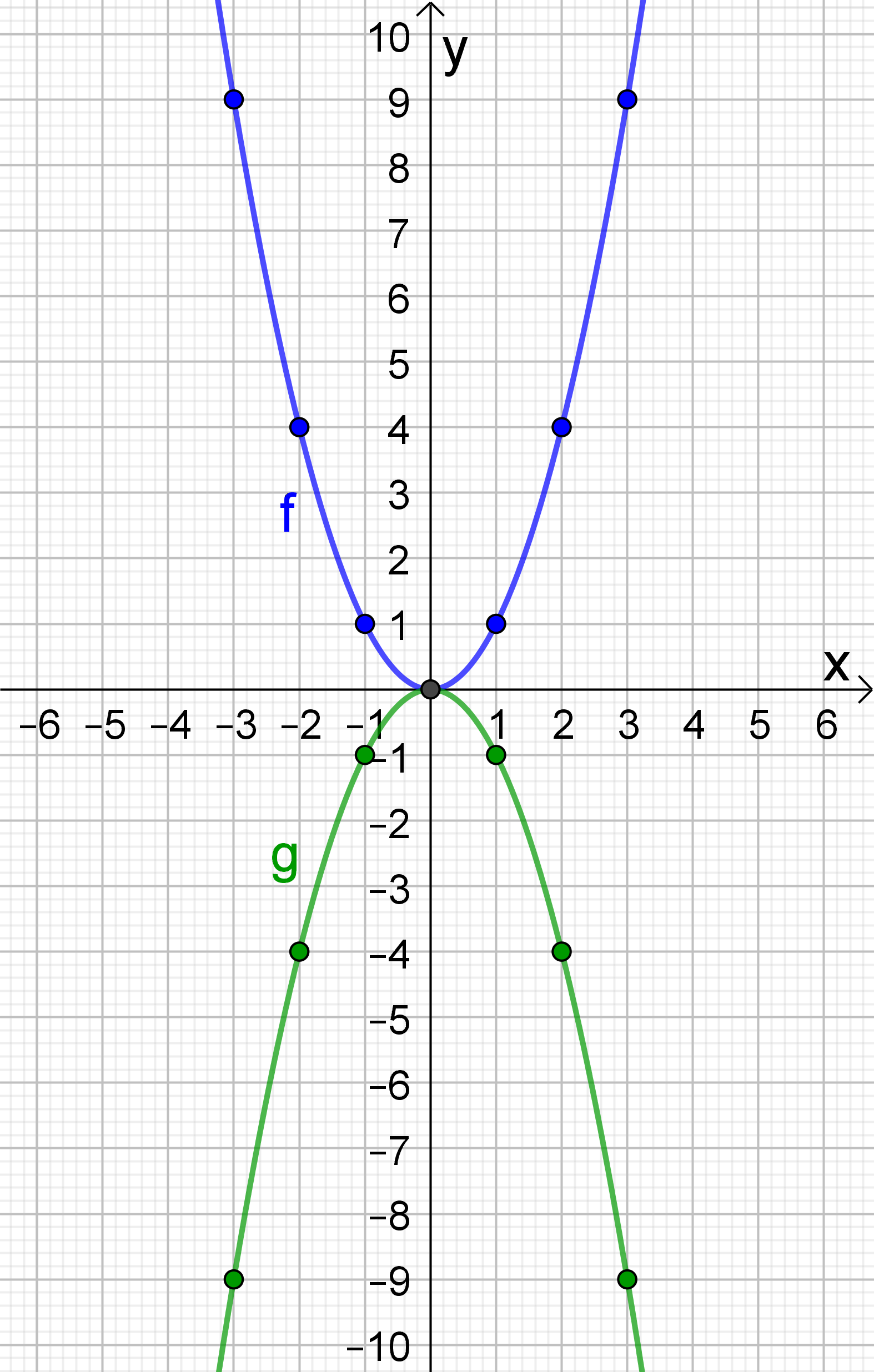
We noemen de grafieken van de functies f(x) = x² en g(x) = -x² parabolen.

f(x) = x²

De grafiek is een dalparabool.
Het laagste punt van de grafiek van f is (0,0).
We noemen dit punt de top van de parabool.
De functie bereikt een minimum voor x = 0.
De symmetrieas van de grafiek is de y-as met vergelijking x = 0.

g(x) = -x²

De grafiek is een bergparabool.
Het hoogste punt van de grafiek van g is (0,0).
We noemen dit punt de top van de parabool.
De functie bereikt een maximum voor x = 0.
De symmetrieas van de grafiek is de y-as met vergelijking x = 0.

Je kan de grafiek van g(x) = -x² verkrijgen uit de grafiek van f(x) = x² door de grafiek van f te spiegelen om de x-as.

De functies f(x) = x² en g(x) = -x²

Lesinhoud

Extra materiaal