Bereik

Het bereik van een functie is de verzameling van de y-waarden waarvoor er een x-waarde bestaat zodat y = f(x).

Zie ook

Tweedegraadsfuncties - Herhaling functies - Domein, bereik en nulpunten

Constante functie

Een constante functie is een functie die elk reëel getal x afbeeldt op een constant getal c met .

Zie ook

Tweedegraadsfuncties - Herhaling functies - Constante functies

Domein

Het domein van een functie y = f(x) is de verzameling van alle originelen x waarbij we het beeld y kunnen berekenen.

Zie ook

Tweedegraadsfuncties - Herhaling functies - Domein, bereik en nulpunten

Eerstegraadsfuncties

Een eerstegraadsfunctie is een functie die elk reëel getal x afbeeldt op 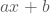met en

Zie ook

Tweedegraadsfuncties - Herhaling functies - Eerstegraadsfuncties

Functie

Een functie is een verband tussen twee variabelen x en y waarbij we voor elke waarde van de input x hoogstens één waarde van de output y kunnen berekenen.

Zie ook

Tweedegraadsfuncties - Herhaling functies - Wat is een functie?

Soorten functies

• Constante functies: Tweedegraadsfuncties - Herhaling functies - Constante functies
• Eerstegraadsfuncties: Tweedegraadsfuncties - Herhaling functies - Eerstegraadsfuncties

Nulpunt

Een nulpunt (of nulwaarde) van een functie is een x-waarde waarvoor de functiewaarde nul is.

Zie ook

Tweedegraadsfuncties - Herhaling functies - Domein, bereik en nulpunten

Nulwaarde

Een nulwaarde (of nulpunt) van een functie is een x-waarde waarvoor de functiewaarde nul is.

Zie ook

Tweedegraadsfuncties - Herhaling functies - Domein, bereik en nulpunten

Richtingscoëfficiënt

De richtingscoëfficiënt van een rechte in een vlak met een rechthoekig xy-assenstelsel is de tangens van de hoek die de rechte maakt met de positieve x-as. De richtingscoëfficiënt is een maat voor de helling van de lijn ten opzichte van de x-as.

Als de rechte gegeven wordt door de vergelijking is het getal a de richtingscoëfficiënt. De richtingscoëfficiënt kan worden gevonden door het differentiequotiënt te nemen van twee punt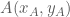en en op de rechte:

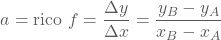
Zie ook

Tweedegraadsfuncties - Herhaling functies - Eerstegraadsfuncties

Verticale lijntest

Een vlakke kromme is de grafiek van een functie als elke verticale rechte hoogstens één snijpunt heeft met deze grafiek.
Men spreekt over de verticale lijntest.

Zie ook

Tweedegraadsfuncties - Herhaling functies - Verticale lijntest