Tweedegraadsfuncties - De functies f(x) = ax² + bx + c - Symmetrieas en top

Symmetrieas en top

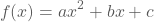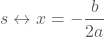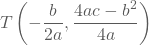De grafiek van de functie $f(x)=ax²+bx+c$ is een parabool met symmetrieas $x=-b/(2a)$ en top $(-b/(2a),(4ac-b²)/(4a)$ .

Voorbeeld

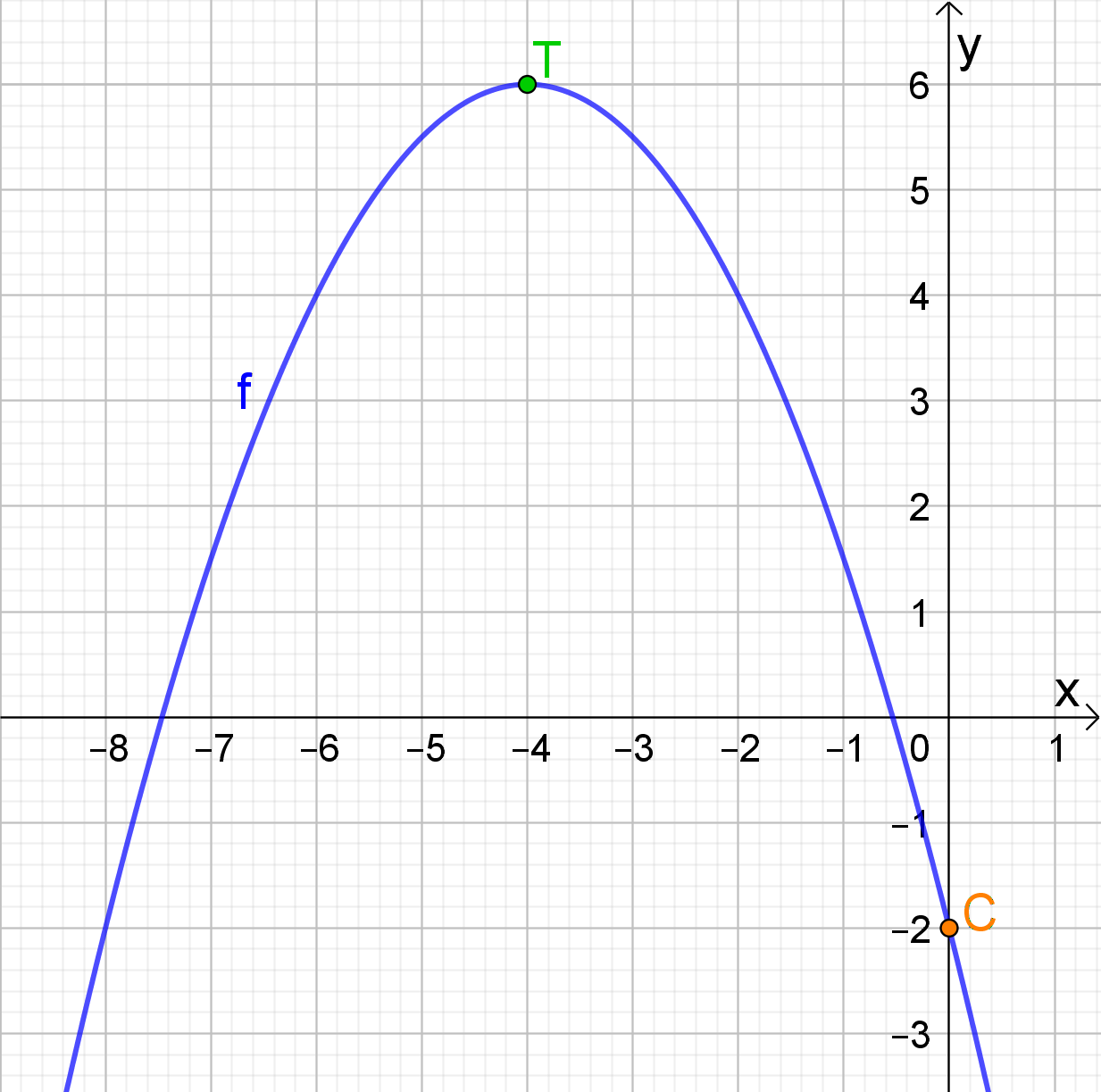
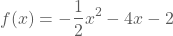Bepaal de top en de symmetrieas van de grafiek van de functie f met voorschrift $f(x)=-0.5x²-4x-2$ .

Top

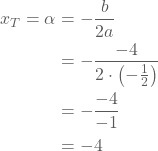
$x=alpha=-4$
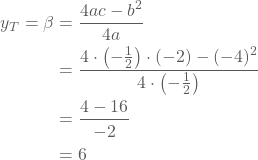
$y=beta=6$

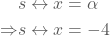
De coördinaat van de top is dus T(-4,6).

Symmetrieas
$S.A.: x=-4$

Merk op

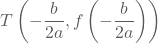
In de praktijk berekenen we de y-coördinaat van de top zonder gebruik te maken van de formule. Het is immers eenvoudiger om de functiewaarde van de x-coördinaat van de top te bepalen: $(-b/(2a),f(-b/(2a)))$
In het voorgaande voorbeeld wordt dit:

$f(-4)=6$
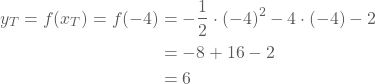
Uit het voorschrift 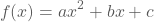$f(x)=ax²+bx+c$ kunnen we rechtstreeks het snijpunt met de y-as afleiden, nl. (0, c). Immers f(0) = c.

×

Lesinhoud

Extra materiaal