Contact
4e jaar 5u wiskunde 5e jaar 4u wiskunde
Begrippenlijst Home
Tweedegraadsfuncties Rekenen met veeltermen Elementaire functies Rijen Driehoeksmeting De cirkel Analytische meetkunde Ruimtemeetkunde Kansrekenen

Tweedegraadsfuncties - De functies f(x) = ax² + bx + c - Verband met f(x) = a(x - α)² + β: inleiding

Verband met f(x) = a(x - α)² + β: inleiding

Van y = a(x - α)² + β naar y = ax² + bx + c

We kunnen eenvoudig overgaan van de grafische vorm y=a(x-alpha)²+beta naar de standaarvorm y=ax²+bx+c door het merkwaardig product (x-alpha)² uit te werken.

Herinner je de volgende merkwaardige producten:

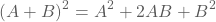
(A+B)²=A²+2AB+B²
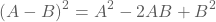
(A+B)²=A²-2AB+B²

Voorbeeld

voorbeeld

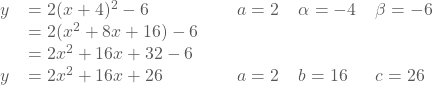
Van y = ax² + bx + c naar y = a(x - α)² + β

Het omgekeerde is wat minder voor de hand liggend. We illustreren de denkwijze aan de hand van een voorbeeld.

Voorbeeld

Parameter a is dezelfde in de standaardvorm en de grafische vorm. Deze waarde plaatsen we eerst voorop.

y=2x²+16x+26=2(x²+8x+13)

Nu proberen we een merkwaardig product te bekomen.

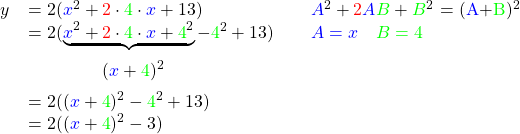
y=2x²+16x+26=2((x+4)²-3)

Tenslotte brengen we de 2 terug binnen de haakjes.

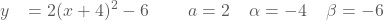
y=2x²+16x+26=2(x+4)²-6

Deze werkwijze is niet zo handig in gebruik. Daarom zullen we in het volgende deeltje formules afleiden om eenvoudig te kunnen overgaan van de standaardvorm y=ax²+bx+c naar de grafische vorm y=a(x-alpha)²+beta.