Eerstegraadsfuncties

Definitie

Een eerstegraadsfunctie is een functie die elk reëel getal x afbeeldt op 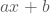met en .

Merk op

De exponent van x is 1, vandaar de naam eerstegraadsfunctie.

Voorstelling

Functievoorschrift

Merk op

• We kunnen het functievoorschrift ook noteren als .
• Vaak worden de letters m en q gebruikt: .
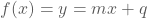• Eerstegraadsfuncties worden ook wel lineaire functies genoemd.

Tabel

Bij elke gelijke toename van een origineel x hoort een gelijke toename van de functiewaarde y.

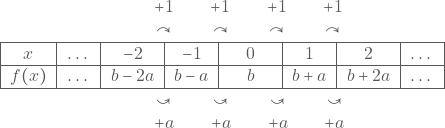
Telkens x toeneemt met 1 eenheid, zal

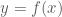
• toenemen met a eenheden als a > 0,
• afnemen met |a| eenheden als a < 0.

Grafiek

De grafiek van de functie is een rechte met richtingscoëfficiënt a die door het punt met coördinaat (0,b) gaat en

• niet evenwijdig loopt met de x-as (a = 0 en dus y = b → zie constante functie),
• niet evenwijdig loopt met de y-as (geen functie → zie verticale lijntest).

Deze rechte kan stijgen (a > 0) of dalen (a < 0). Ook in de grafiek zien we dat als x met 1 eenheid toeneemt, 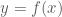zal toenemen met a eenheden als a > 0 en afnemen met |a| eenheden als a < 0.

De rechte is steiler naarmate |a| groter is. De richtingscoëfficiënt is dus een maat voor de steilheid van de rechte. De richtingscoëfficiënt wordt ook wel het hellingsgetal of de gemiddelde verandering genoemd.

a > 0	a < 0

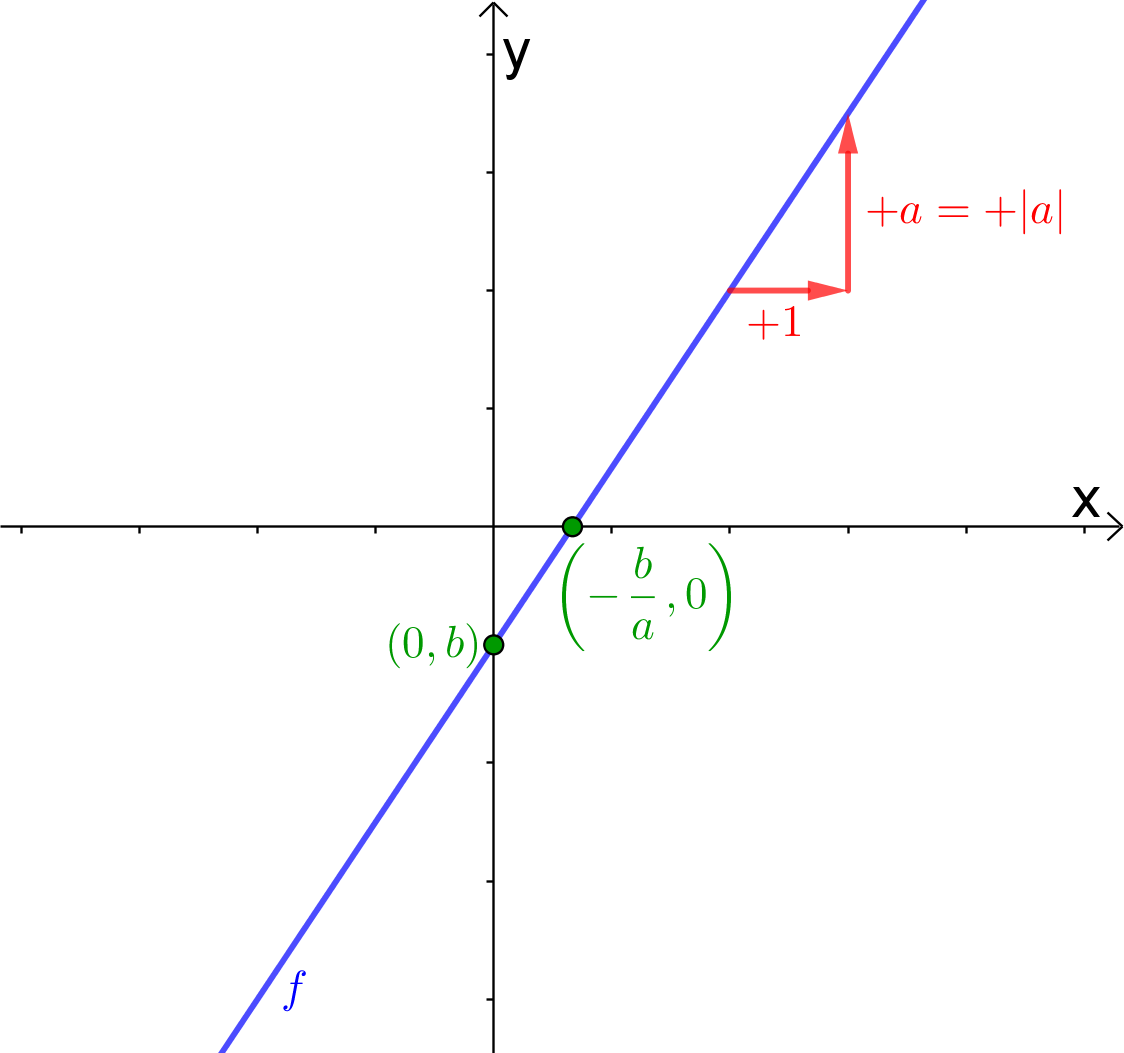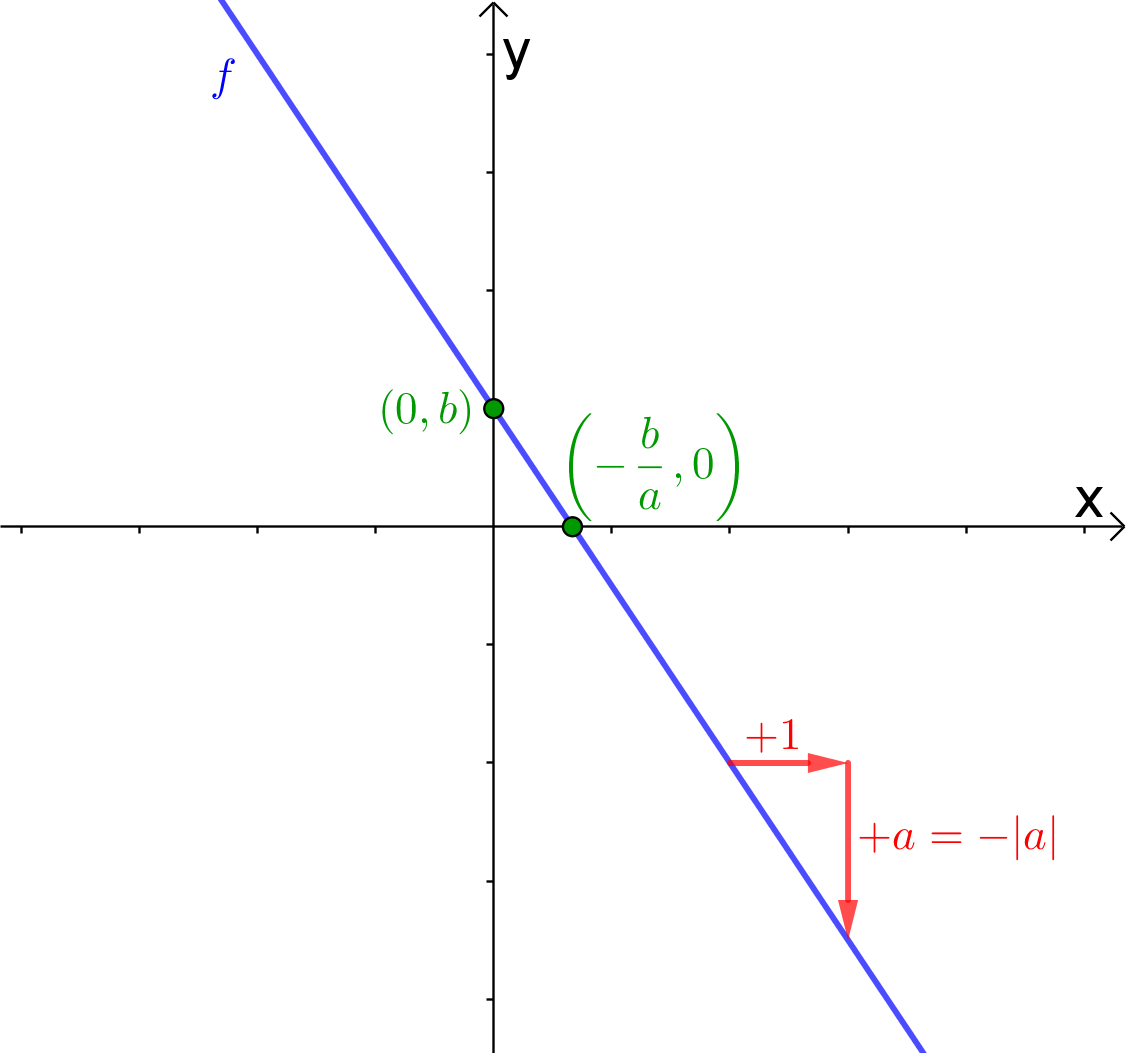Snijpunt met de x-as

Wanneer een functie de x-as snijdt, is de functiewaarde (y-waarde) 0. In het functievoorschrift van onze rechte stellen we dus y = 0

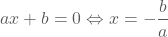
We lossen dus een eerstegraadsvergelijking op. Het snijpunt met de x-as heeft als coördinaat .

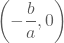Snijpunt met de y-as

Wanneer een functie de y-as snijdt, is de waarde van x gelijk aan 0. In het functievoorschrift van onze rechte stellen we dus x = 0

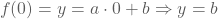
Het snijpunt met de y-as heeft als coördinaat .

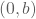Als b = 0, dan is y = ax en gaat de rechte door de oorsprong.

Opmerking

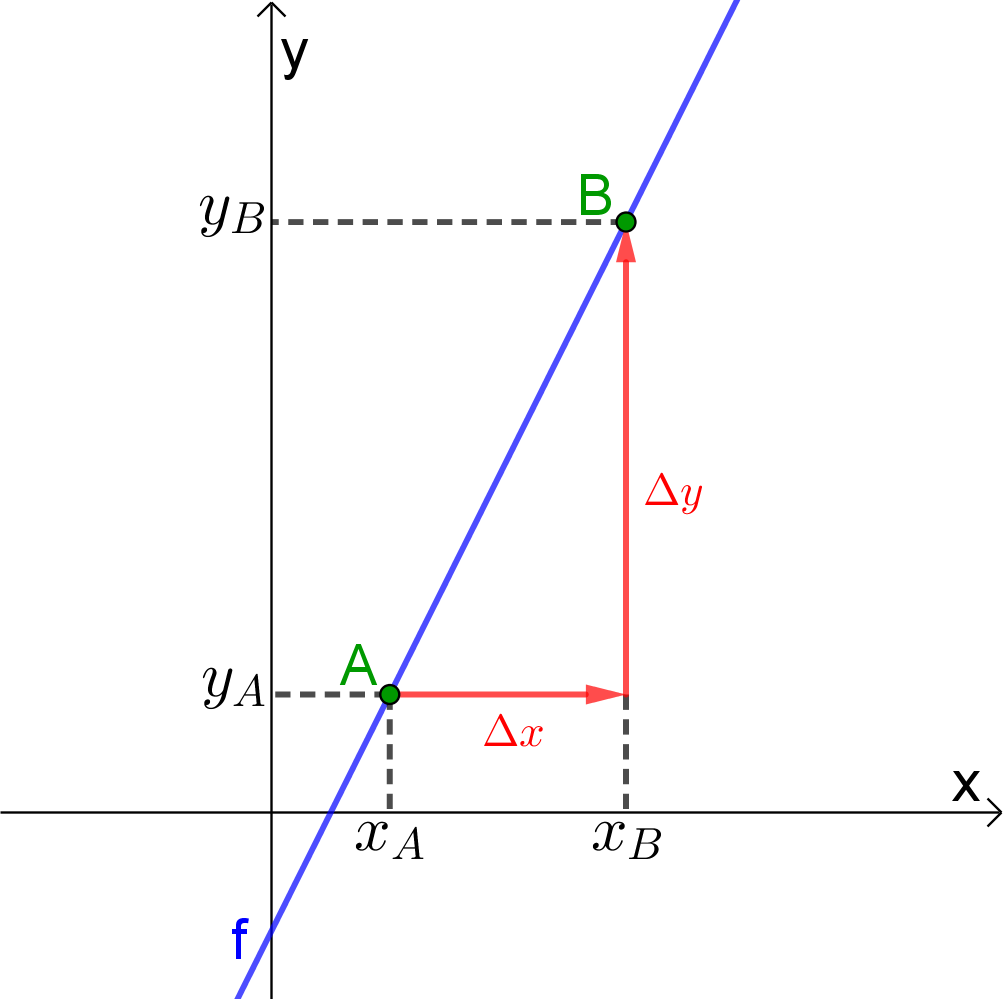
Het is niet altijd mogelijk om de verandering van de y-waarde eenvoudig af te lezen van de grafiek als de x-waarde met 1 toeneemt. We kunnen ook willekeurig twee punt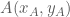en en nemen die tot de rechte f met voorschrift 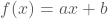(met en ) behoren. De richtingscoëfficiënt a kunnen we dan berekenen als volgt:

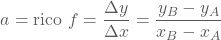
Kenmerken

	a > 0	a < 0
Domein
Bereik
Nulpunten
Snijpunt x-as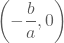
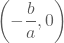Snijpunt y-as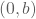
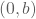Verloopschema
Tekentabel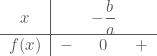