Tweedegraadsfuncties - Herhaling functies - Eerstegraadsfuncties - Oefeningen

Oefeningen

Oefening 1

De tabellen horen bij eerstegraadsfuncties.

x	...	-3	-2	-1	0	1	...
f(x)	...	-7	-2	3	8	13	...

x	...	3	4	5	6	7	...
g(x)	...	13	9	5	1	-3	...

Bepaal de richtingscoëfficiënt van de grafiek van elke functie.
Bepaal het voorschrift van elke functie.

De functie f is een eerstegraadsfunctie. We stellen dus .
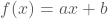- Als de x-waarden met 1 toenemen, nemen de y-waarden toe met 5. Dus de richtingscoëfficiënt a = 5.
- Het punt met coördinaat (0,8) behoort tot de functie, dus b = 8.
Het functievoorschrift is dus $f(x)=5x+8$ .
De functie g is een eerstegraadsfunctie. We stellen dus .
- Als de x-waarden met 1 toenemen, nemen de y-waarden af met 4. Dus de richtingscoëfficiënt a = -4.
- Het functievoorschrift wordt dan $g(x)=-4x+b$ . We kunnen vervolgens een punt invullen om de waarde van b te bepalen. Neem bv. het punt met coördinaat (3,13). Dan geldt:
  $g(3)=13$
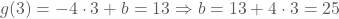
Het functievoorschrift is dus $g(x)=--4x+25$ .

Oefening 2

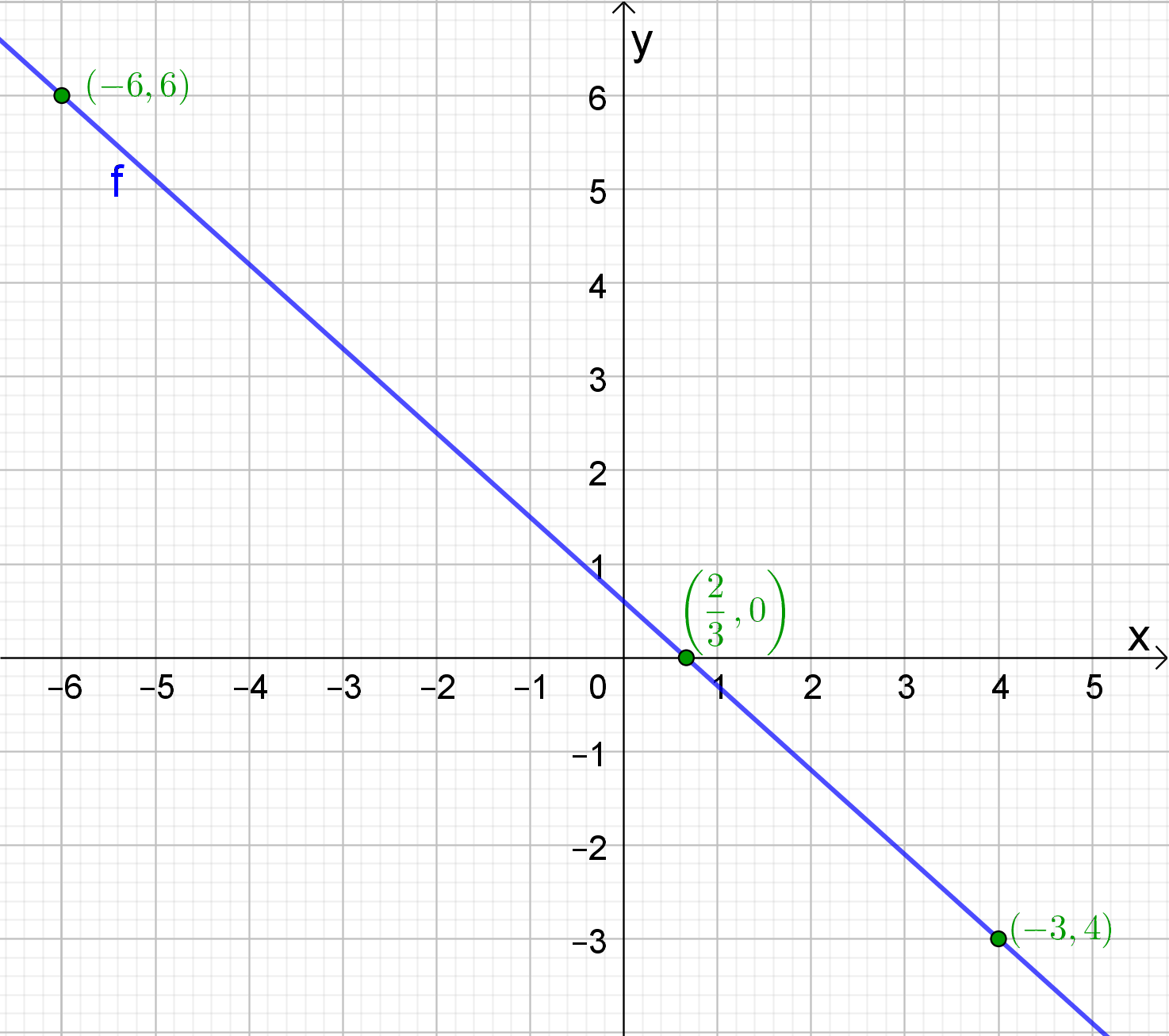
Beschouw de grafiek van de eerstegraadsfunctie f.

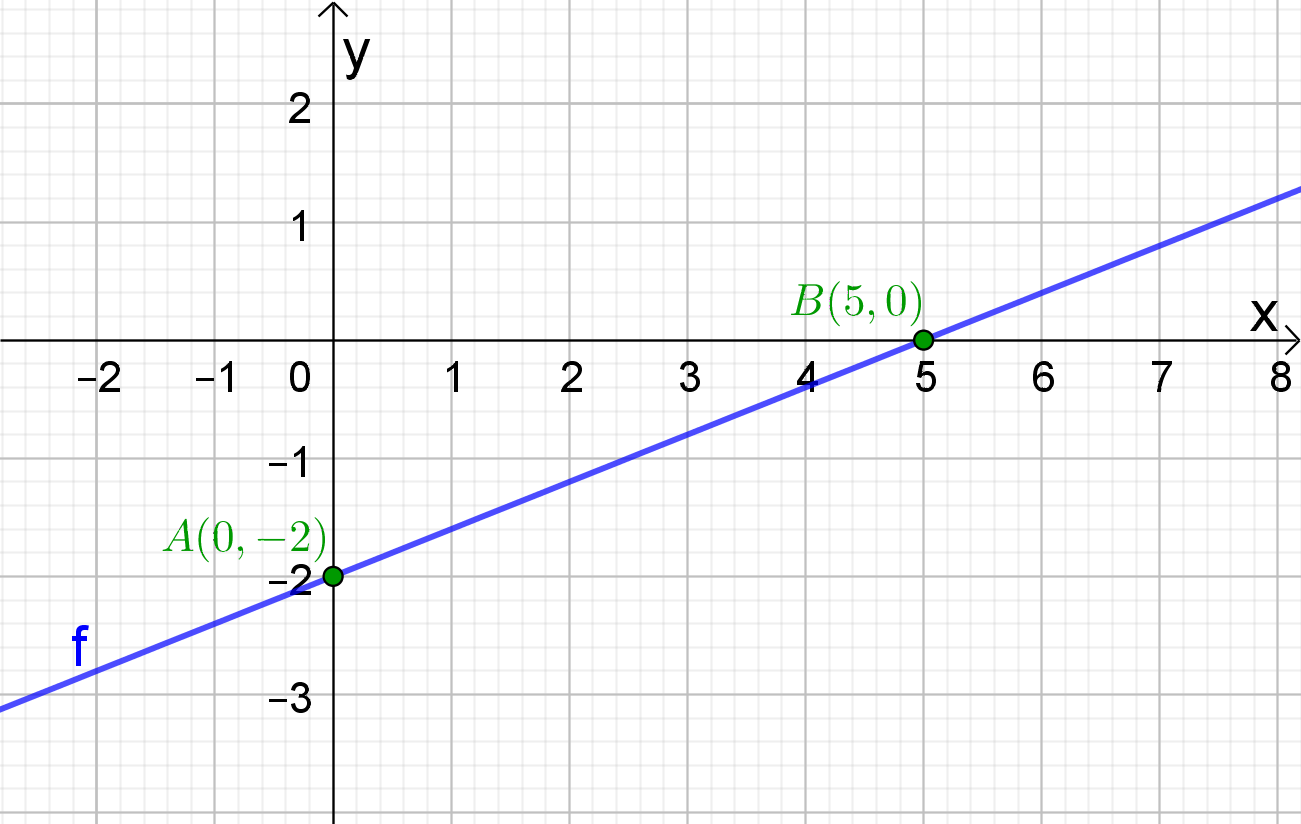
Bepaal het functievoorschrift.

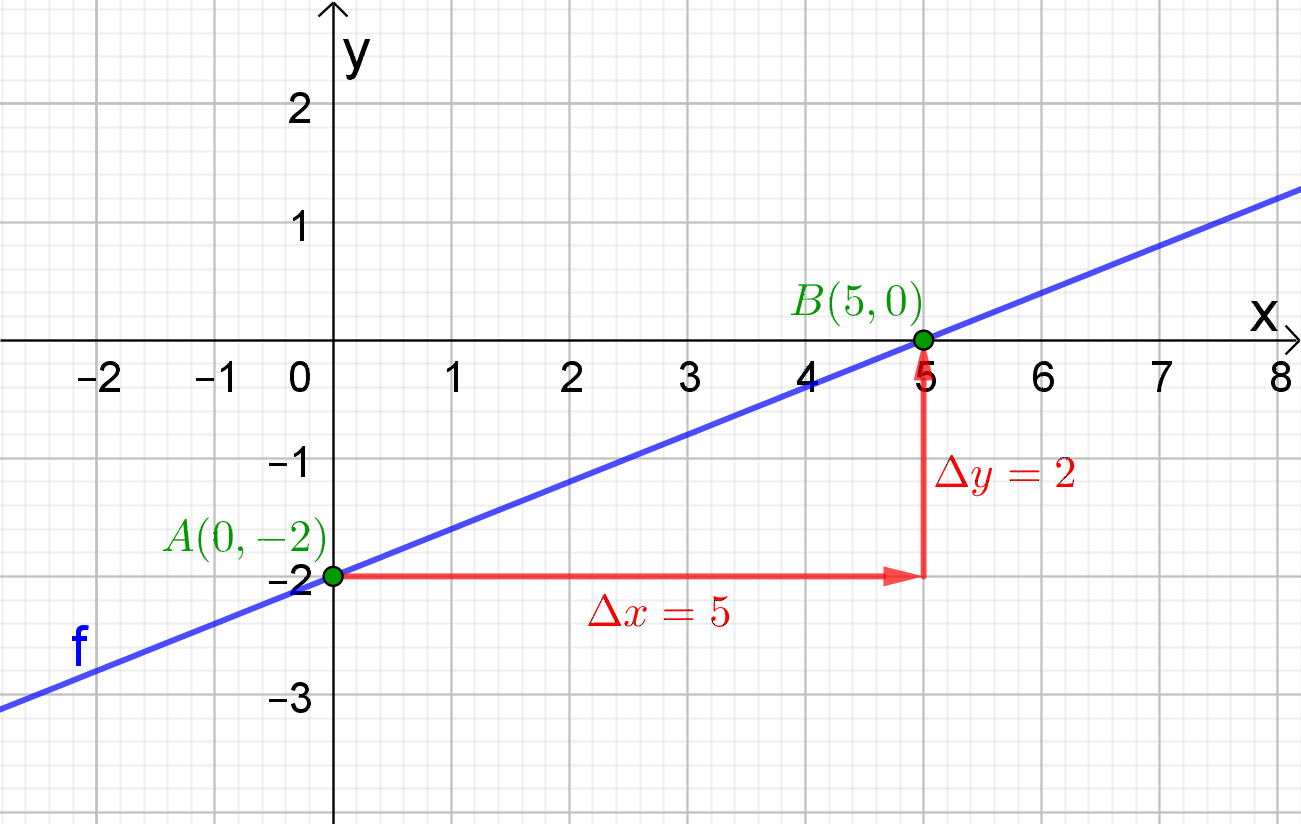
De grafiek stelt een rechte voor. We stellen 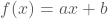$f(x)=ax+b$ . De grafiek gaat door het punt A(0,-2), dus b = -2.

Met behulp van de punten A en B kunnen we nu de richtingscoëfficiënt berekenen.

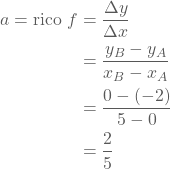
Het functievoorschrift wordt dan 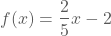$g(x)=(2/5)x-2$ .

Oefening 3

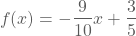Gegeven is de functie f met voorschrift $f(x)=-(9/10)x+3/5$ .

Gevraagd:

Bereken de functiewaarde voor x = -6.
Bepaal het origineel van -3.
Bereken het nulpunt van deze functie.
Voor welke waarden van x ligt de grafiek van f onder de x-as?

In het functievoorschrift vervangen we x door -6:

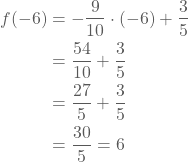
De functiewaarde voor x = -6 is dus 6.
We bepalen de waarde van x waarvoor y = -3:

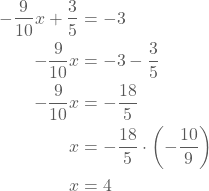
Het origineel van -3 is 4.
Om het nulpunt van de functie f te bepalen, stellen we y = 0:

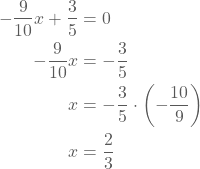
Het nulpunt van de functie is x = ²/₃.

We lossen de ongelijkheid 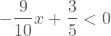$-9/10x+3/5 strikt kleiner dan 0$ op.

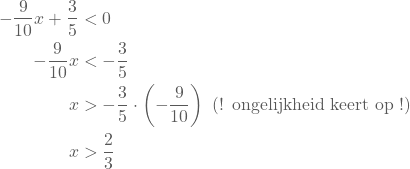
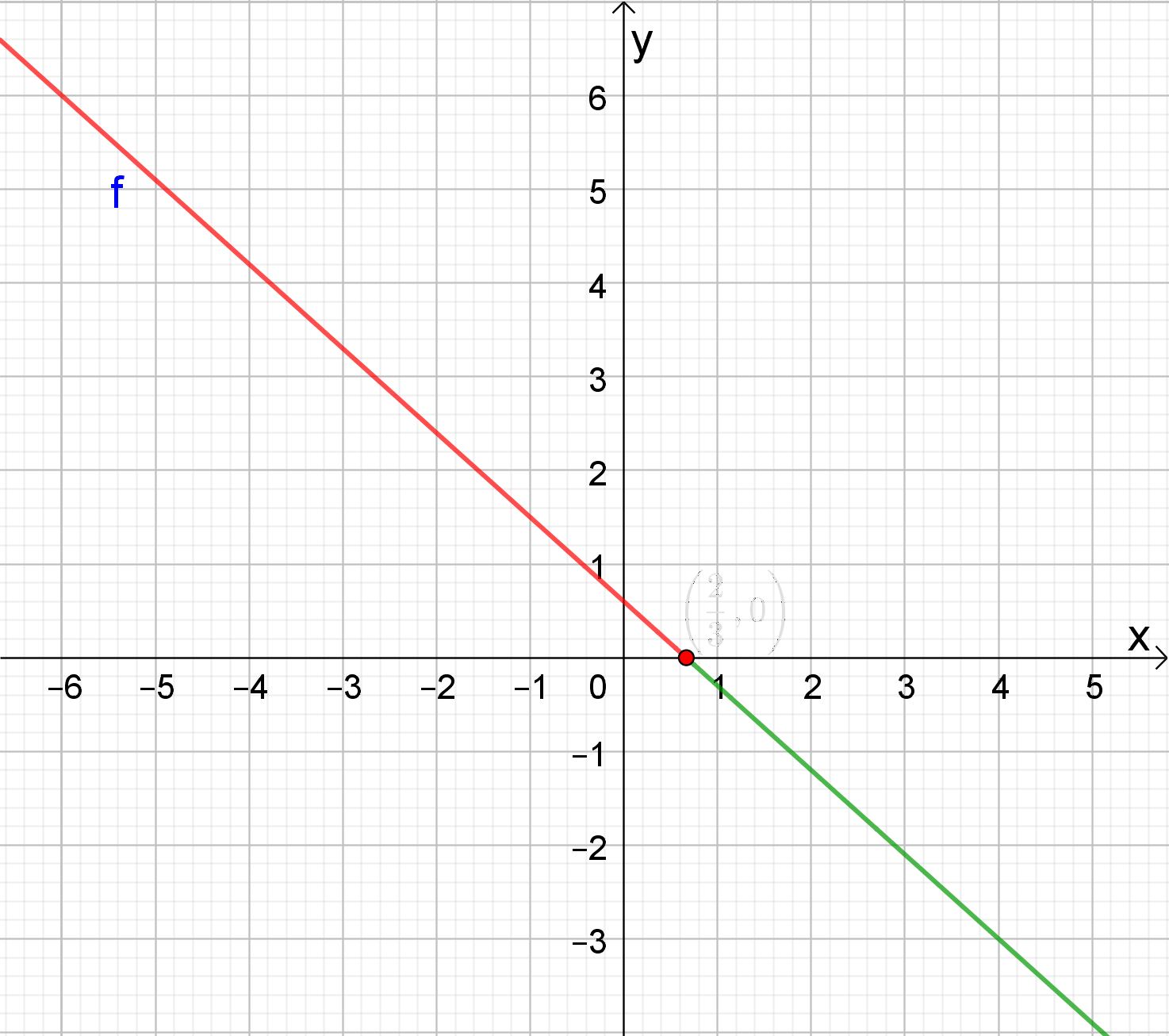
We kunnen ook nog op een alternatieve manier te werk gaan. We hebben het nulpunt reeds berekend in een vorig puntje. De richtingscoëfficiënt van de functie f is negatief. De rechte is dus dalend. Met deze gegevens kunnen we de tekentabel opstellen en de ongelijkheid oplossen.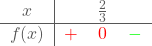 Uit de tekentabel kunnen we aflezen dat de grafiek van f onder de x-as ligt als x > ²/₃.

Oefening 4

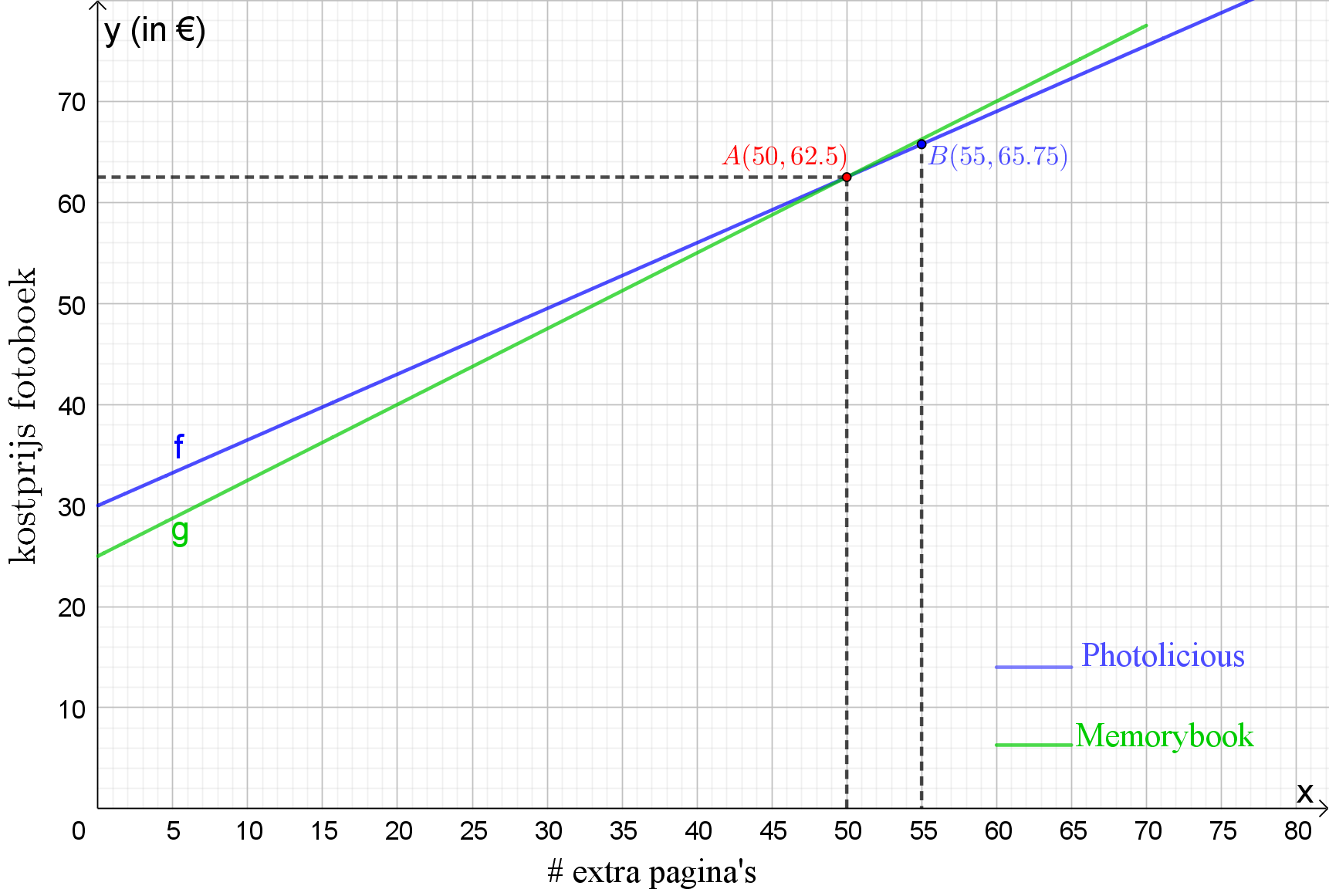
Jonas maakt graag foto's op reis. Eenmaal terug in het land wil hij een fotoboek maken. Hij vergelijkt de prijzen bij twee webshops. Bij 'Photolicious' bedraagt de basisprijs voor een fotoboek met 20 pagina's €30. Het fotoboek is uit te breiden tot 100 bladzijden en per extra bladzijde betaal je €0,65. Bij 'Memorybook' bedraagt de basisprijs voor een fotoboek €25. In deze basisprijs zijn eveneens 20 pagina's inbegrepen. Bij deze webshop is het fotoboek uit te breiden tot 90 bladzijden en per extra bladzijde betaal je €0,75.

Stel de voorschriften op van de functies die voor elke webshop de kostprijs y van het album geeft (in €) in functie van het aantal extra pagina's x.
Bij hoeveel extra pagina's zijn beide fotoboeken even duur?
Jonas maakt een album met 75 pagina's. Welke webshop kiest hij als hij de voordeligste prijs wil en hoeveel betaalt hij dan?

Bij beide webshops neemt de kostprijs van een fotoboek met een vast bedroeg toe telkens we een pagina toevoegen. Er is dus sprake van lineaire groei. Beide voorschriften zijn dus van de vorm .
- Bij 'Photolicious' betalen we €0,65 voor elke extra pagina. De richtingscoëfficiënt is dus a = 0,65. Nemen we geen extra pagina's (x = 0), dan betalen we €30, dus b = 30.
  Het voorschrift is dan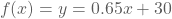 $f(x)=y=0.65x+30$ .
- Bij 'Memorybook' betalen we €0,75 voor elke extra pagina. De richtingscoëfficiënt is dus a = 0,75. Nemen we geen extra pagina's (x = 0), dan betalen we €25, dus b = 25.
  Het voorschrift is dan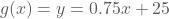 $f(x)=y=0.75x+25$ .
De fotoboeken zijn even duur als 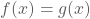$f(x)=g(x)$ . Deze vergelijking lossen we op naar x om het extra aantal pagina's in dit geval te kennen. 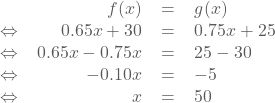Als Jonas 50 extra pagina's toevoegt dan zijn de fotoboeken van beide webshops even duur.
Jonas maakt een album met 75 pagina's. Dat betekent dat hij 55 pagina's extra toevoegt aan het standaard fotoboek (dus x = 55). Uit het voorgaande weten we dat als je minder dan 50 pagina's toevoegt 'Memorybook' goedkoper is. Voeg je meer dan 50 pagina's toe, dan is 'Photolicious' goedkoper. Jonas kiest dus voor 'Photolicious'. We kunnen gebruik maken van het functievoorschrift om de kostprijs te berekenen.
Jonas betaalt dan €65.75 voor een fotoboek van 'Photolicious'.
Als Jonas kiest voor 'Memorybook' dan betaalt hij €66.25:

Oefening 5

In 1724 bedacht Gabriel Fahrenheit een temperatuurschaal die nu nog steeds vooral in de Verenigde Staten gebruikt wordt. In 1742, definieerde Anders Celsius de temperatuurverdeling in graden Celsius. We kunnen graden Celsius omzetten in Fahrenheit met behulp van de omzettingsformule

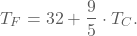
Wat is de smelttemperatuur van water uitgedrukt in graden Fahrenheit?
Als de temperatuur toeneemt met één graad Celcius, hoeveel graden Fahrenheit neemt de temperatuur dan toe?
Kan een temperatuur gelijk zijn bij beide temperatuursschalen? Zo ja, bij welke temperatuur is dat?

De smelttemperatuur van water uitgedrukt in graden Celcius is T_C = 0 °C.
Dit invullen in de omzettingsformule, levert T_F = 32 °F.
De omzettingsformule komt overeen met de eerstegraadsfunctie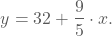 $y=32+9/5.x$
De y-coördinaat van het snijpunt met de y-as, is 32 en komt overeen met de smelttemperatuur van ijs.
De richtingscoëfficiënt is ⁹/₅. Dit betekent dat een toename van de temperatuur met één graad Celsius overeenkomt met een toename van ⁹/₅ = 1.8 graden Fahrenheit.
We gaan na wanneer T_F = T_C. Dit komt neer op het oplossen van eerstegraadsvergelijking. 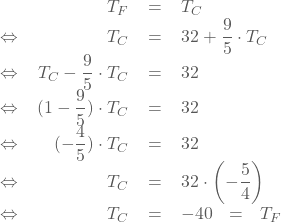Dus bij -40 graden is de temperatuur gelijk bij beide schalen.