Tweedegraadsfuncties - Herhaling functies - Eerstegraadsfuncties - Opstellen van het functievoorschrift

Opstellen van het functievoorschrift van een eerstegraadsfunctie

Voorbeeld 1

Beschouw de grafiek van de functie f.

voorbeeld 1

Bepaal het functievoorschrift op basis van de gegeven grafiek.

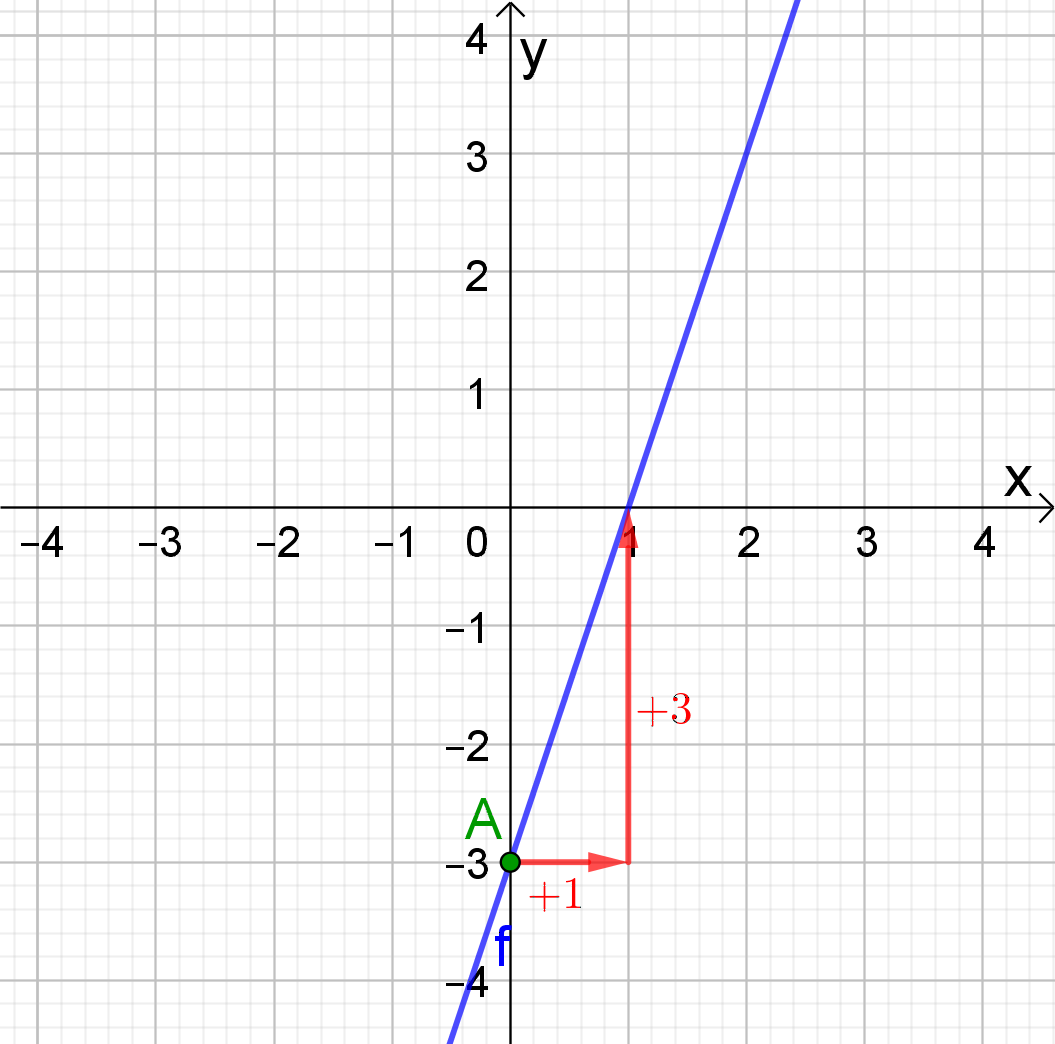
voorbeeld 1

De grafiek stelt een rechte voor. We stellen 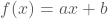$f(x)=ax+b$ .

We kunnen a en b eenvoudig bepalen gebruik makende van de grafische betekenis van deze parameters

Het snijpunt met de y-as kunnen we aflezen: dit is A(0,-3). dus b = -3.

Daarnaast behoort ook het punt (1,0) tot de rechte. Neemt de x-waarde dus met 1 toe, dan neemt de y-waarde met 3 toe. De richtingscoëfficiënt is 3, dus a = 3.

Het functievoorschrift wordt dan 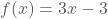$f(x)=3x-3$ .

Voorbeeld 2

Beschouw de rechte die gaat door de punten 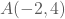$A(-2,4)$ en $B(-1,1)$

voorbeeld

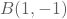
Bepaal het functievoorschrift op basis van de gegeven punten.

Methode 1

Het voorschrift is van de vorm $a in R zonder 0$ en bevat de punten A en B.

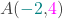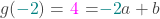
Het punt $A(-2,4)$ behoort tot g, dus $g(-2)=4$ $b=4+2a$ (1)
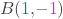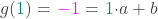
Het punt $B(-1,1$ behoort tot g, dus $g(1)=-1$ $b=-2-a$ (2)

Uit (1) en (2) volgt:

a=-5/3

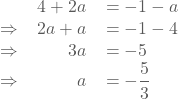
We bekomen dan 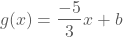$g(x)=(-5/3)x+b$ .

We kunnen a nu invullen in (1) of (2) om b te bepalen. Vullen we a in in (1), dan bekomen we:

b=2/3

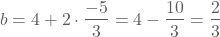
Het functievoorschrift wordt dan 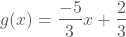$g(x)=(-5/3)x+2/3$ .

Methode 2

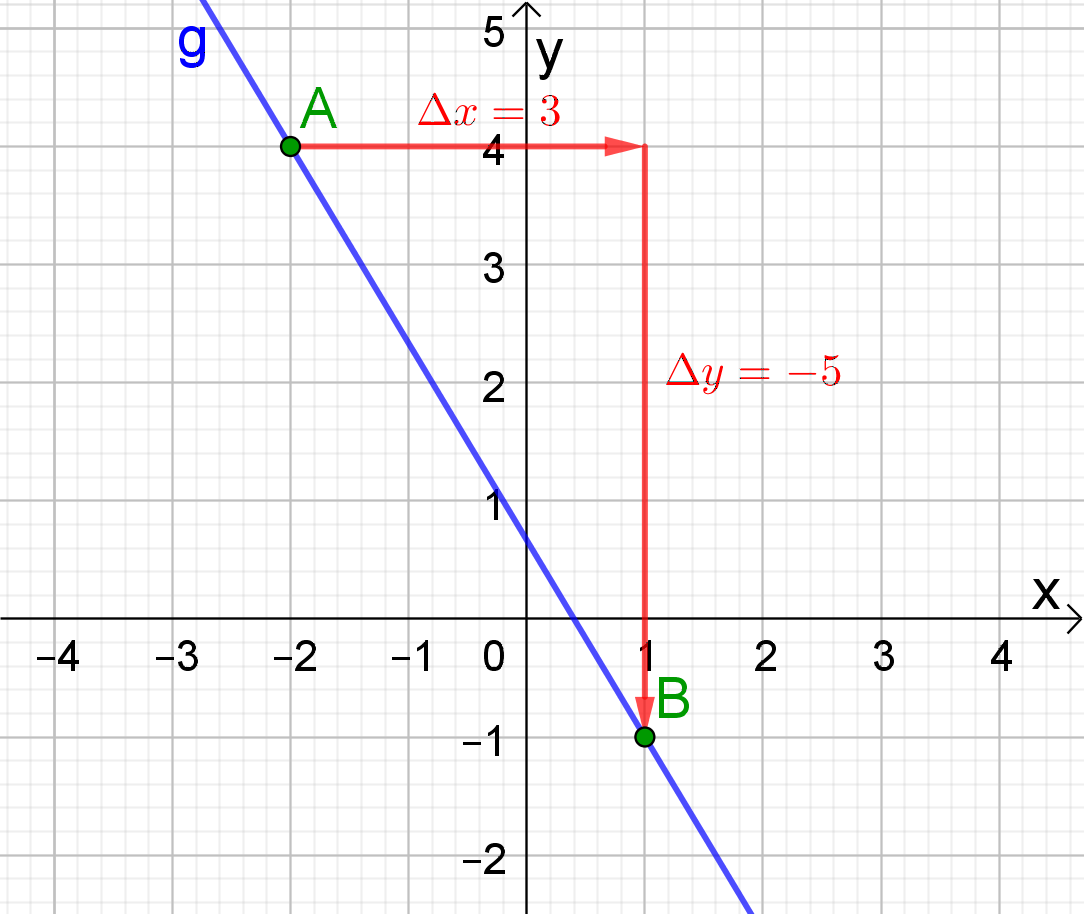
voorbeeld 2

Het voorschrift is van de vorm $a in R zonder 0$ . We kunnen de richtingscoëfficiënt a en het snijpunt met de y-as (0,b) niet eenvoudig aflezen.

We berekenen eerst de richtingscoëfficiënt a:

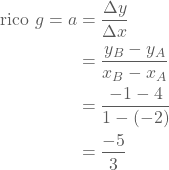
voorbeeld 2

We bekomen dan 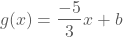$g(x)=(-5/3)x+b$ .

We kunnen nu b vinden door een punt in te vullen. Bv. punt $B(-1,1)$ .

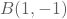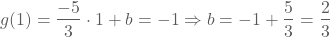
voorbeeld 2

Het functievoorschrift wordt dan 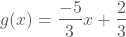$g(x)=(-5/3)x+2/3$ .

De rechte gaat door het punt 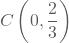$C(0,2/3$ .

×

Lesinhoud

Extra materiaal