Tweedegraadsfuncties - Herhaling functies - Eerstegraadsfuncties - De grafiek tekenen
De grafiek van een eerstegraadsfunctie tekenen
Om de grafiek van een eerstegraadsfunctie te tekenen, kiezen we eerst enkele originelen (x-waarden) waarvan we hun bijhorende functiewaarden (y-waarden) berekenen. We kunnen dit weergeven in een tabel.
Voorbeeld 1
We tekenen de eerstegraadsfunctie 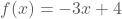 (of
(of 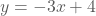 ).
).
We kunnen van enkele originelen hun bijhorende functiewaarden berekenen. Bijvoorbeeld:

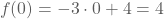
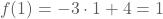
- ...
Handiger is om gebruik te maken van een tabel:
| x | ... | -1 | 0 | 1 | 2 | 3 | ... |
| f(x) | ... | 7 | 4 | 1 | -2 | -5 | ... |
Op basis van bovenstaande koppels kunnen we de grafiek tekenen. We duiden de punten aan in een assenstelsel om ze nadien met een lat te verbinden. In principe volstaat het om ons tot twee punten te beperken. Door twee punten gaat immers juist één rechte.

We kunnen ook gebruik maken van de grafische betekenis van de parameters a en
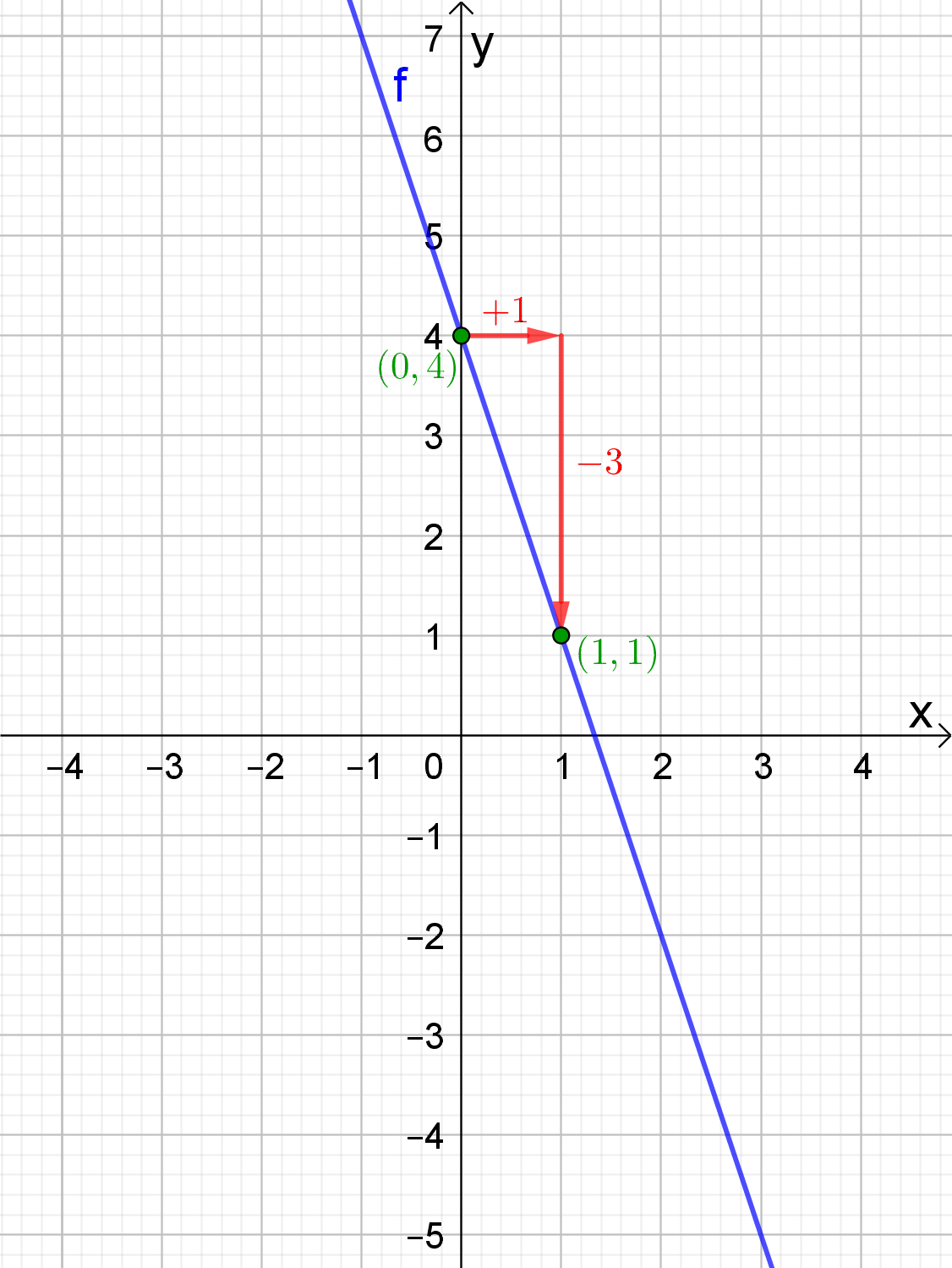
b. De rechte met het functievoorschrift
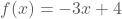 heeft als richtingscoëfficiënt -3 en gaat door het punt (0,4). Als de x-waarde met 1
toeneemt, zal de y-waarde met 3 afnemen. Het punt (1,1) zal dus ook tot de grafiek van de
rechte behoren. Deze 2 punten kunnen we dan met elkaar verbinden.
heeft als richtingscoëfficiënt -3 en gaat door het punt (0,4). Als de x-waarde met 1
toeneemt, zal de y-waarde met 3 afnemen. Het punt (1,1) zal dus ook tot de grafiek van de
rechte behoren. Deze 2 punten kunnen we dan met elkaar verbinden.
Voorbeeld 2
In dit voorbeeld tekenen we de eerstegraadsfunctie 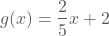 (of
(of 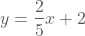 ).
We kunnen opnieuw gebruik maken van de grafische betekenis van de parameters a en
b. De rechte met het functievoorschrift
).
We kunnen opnieuw gebruik maken van de grafische betekenis van de parameters a en
b. De rechte met het functievoorschrift
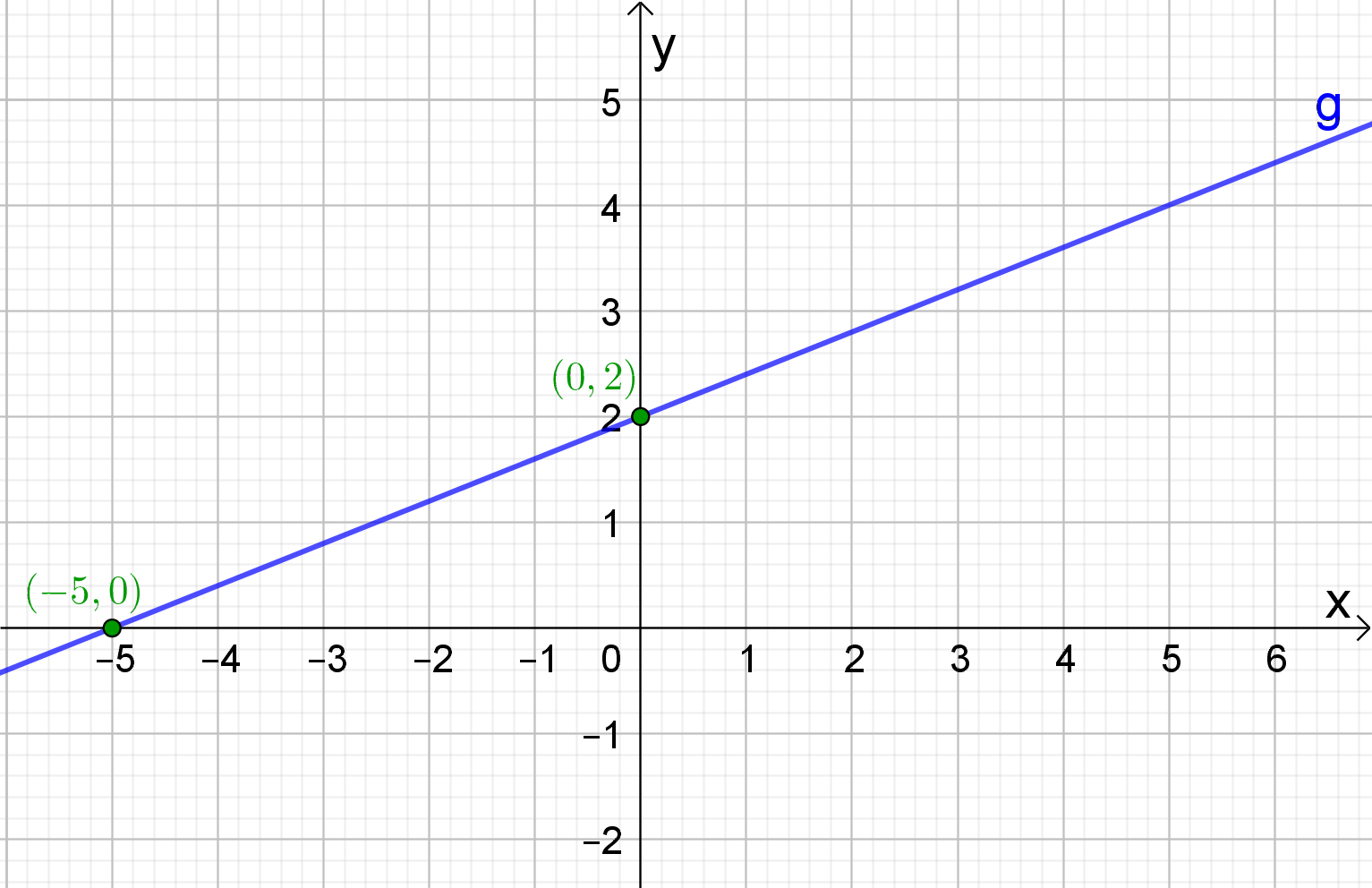
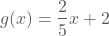 heeft als richtingscoëfficiënt 2/5 en gaat door het punt (0,2). Als de
x-waarde met 5 toeneemt, zal de y-waarde met 2 toenemen.
Het punt (5,4) zal dus ook tot de grafiek van de rechte behoren. Door deze 2 punten kunnen we dan de rechte tekenen.
heeft als richtingscoëfficiënt 2/5 en gaat door het punt (0,2). Als de
x-waarde met 5 toeneemt, zal de y-waarde met 2 toenemen.
Het punt (5,4) zal dus ook tot de grafiek van de rechte behoren. Door deze 2 punten kunnen we dan de rechte tekenen.
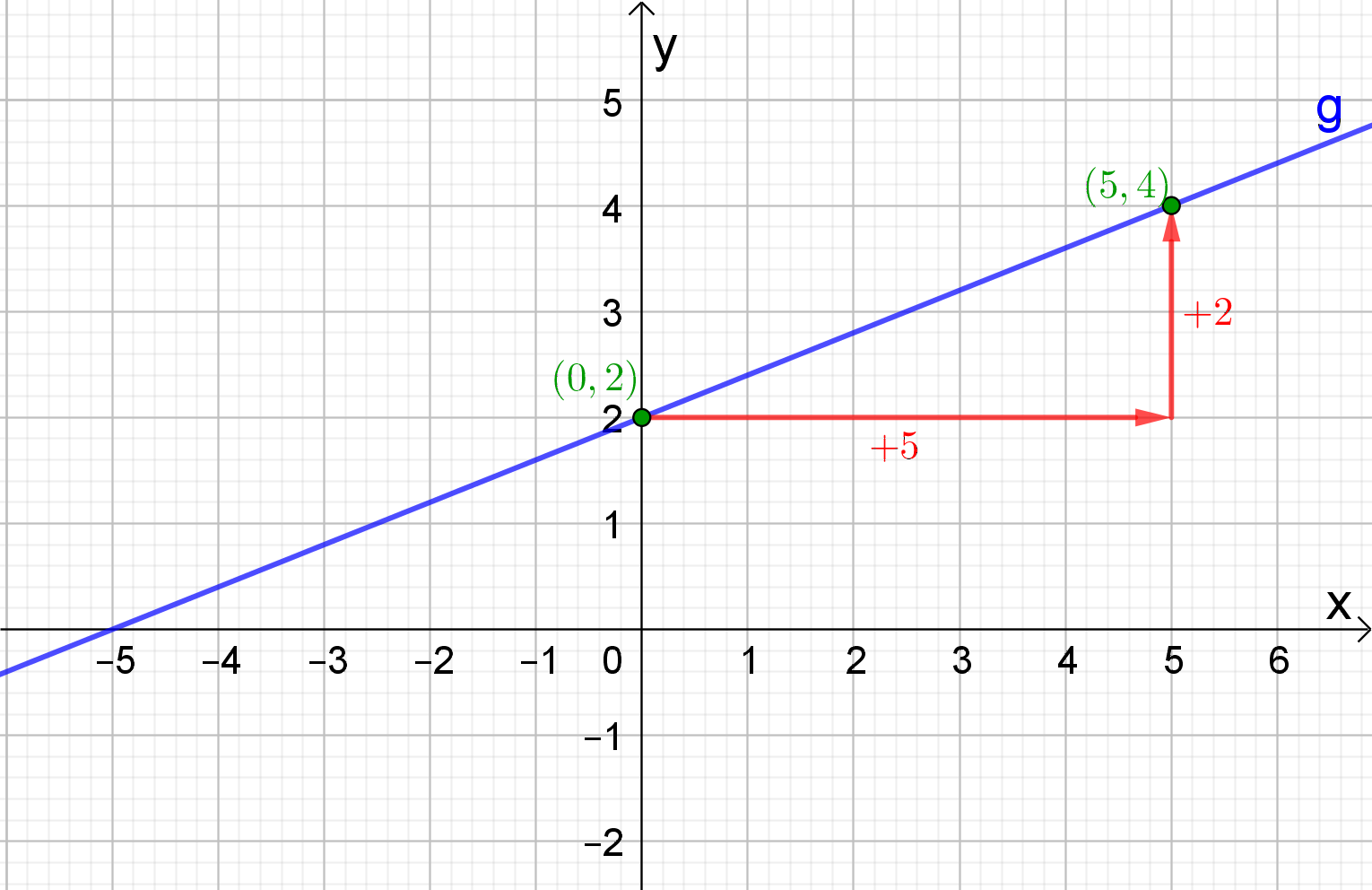
Om de grafiek te tekenen kunnen we ook gebruik maken van de snijpunten met de x- en de de y-as. Het snijpunt met de y kennen we reeds. Dat is (0,2). Het snijpunt met de x-as vinden we door volgende vergelijking op te lossen:
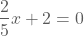
De oplossing bekomen we als volgt:
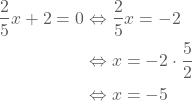
Het snijpunt met de x-as is dus (-5,0). We kunnen dan de rechte tekenen door de punten (-5,0) en (0,2).