Tweedegraadsfuncties - De functies f(x) = a(x - α)² + β
De functies f(x) = a(x - α)² + β
Tenslotte brengen we alle informatie uit de voorgaande deeltjes samen: we bestuderen de grafiek van de functie
.
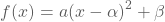Voorbeeld
We bestuderen de grafiek van de functie
.
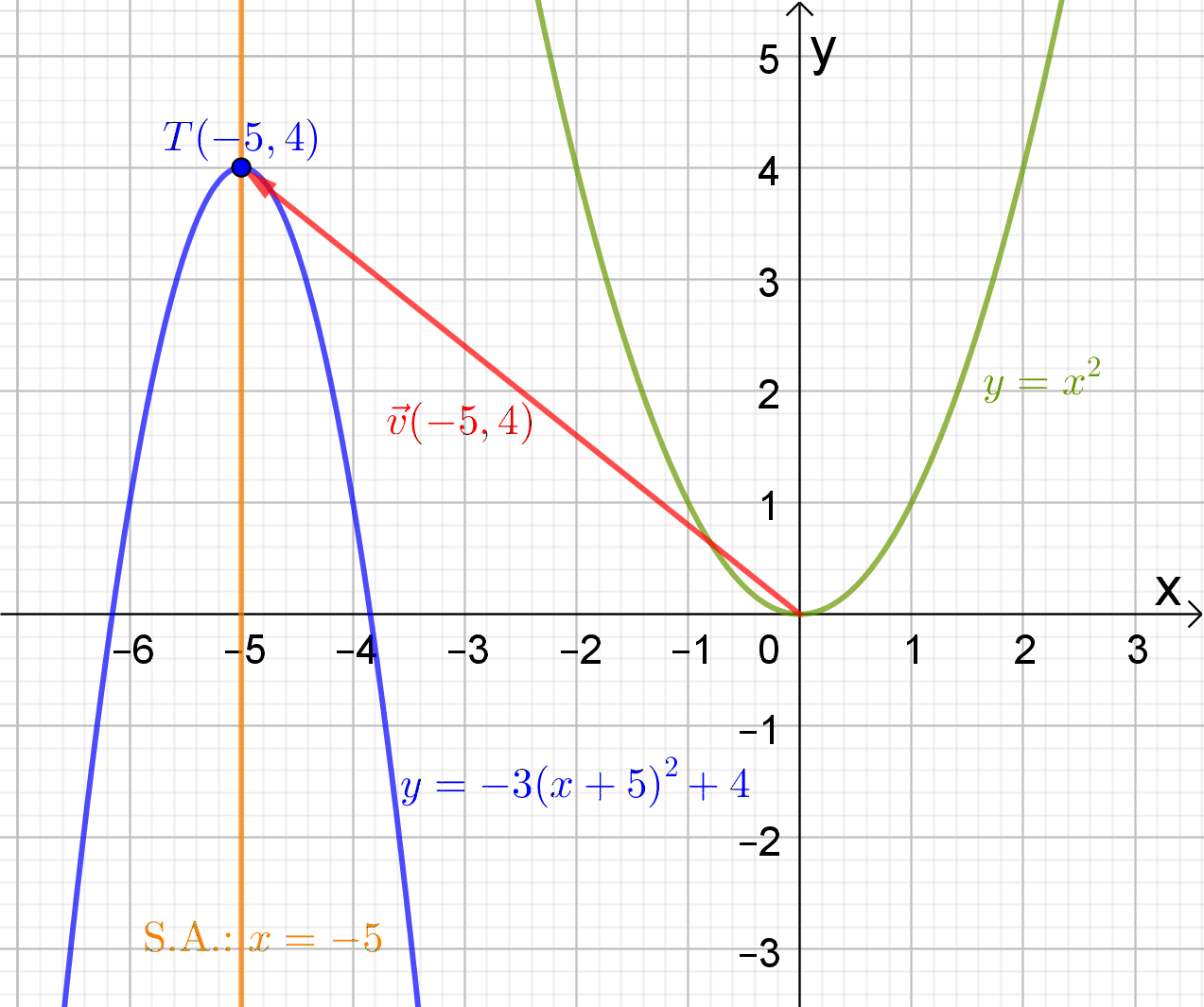
We kunnen de grafiek van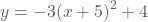 
vinden door op de grafiek van 
achtereenvolgens het effect van a, het effect van α en het effect van β toe te passen.
- Het effect van de parameter a = -3
Er is een verticale uitrekking met factor 3
en aangezien a < 0 is er ook een spiegeling om de x-as. - Het effect van de parameter α = -5
Vervolgens is er een veschuiving over 5 eenheden naar links. - Het effect van de parameter β = 4
Tenslotte is er een verschuiving over 4 eenheden naar boven.
We kunnen ook eenvoudig de coördindaat van de top en de vergelijking van de symmetrieas bepalen.
- De top van de parabool is T(α,β) = T(-5,4).
- De symmetrieas van de grafiek is de verticale rechte met vergelijking x-as.
Ook de grafiek van de functie
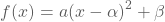noemen we een parabool.
- a > 0: dalparabool 🙂
a < 0: bergparabool 🙁 - De top van de parabool is (α,α).
- De symmetrieas van de grafiek is de verticale rechte met vergelijking x = α.
We vinden de grafiek van de functie
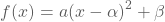door op de grafiek van
achtereenvolgens het effect van a, het effect van α en het effect van β toe te passen.
- Het effect van de parameter a op de grafiek van de functie f:
een verticale uitrekking met factor |a|
als a < 0: + een spiegeling om de x-as. - Het effect van de parameter α op de grafiek van de functie f:
een horizontale verschuiving over |α| eenheden
als α > 0: naar rechts
als α < 0: naar links - Het effect van de parameter β op de grafiek van de functie f:
een verticale verschuiving over |β| eenheden
als β > 0: naar boven
als β < 0: naar beneden
